Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 3.Problemas - Ex. 16
Mostre que independente do valor da carga, conectada aos terminais c-d. temos: e .
Passo 1
Dado o circuito:
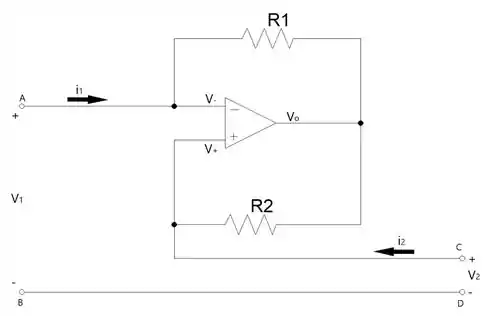
Temos que provar que e que .
Para a primeira verificação, basta analisarmos o circuito e as propriedades de amplificadores operacionais.
Para provar que , temos que ter em mente que . O ponto C no circuito pode ser considerado todo o fio que a ele pertence pois estamos falando de fios ideais. Portanto e logo aplicando o mesmo para o ponto A, . Então chegamos a conclusão que .
Passo 2
Agora vamos provar que , pra isso vamos aplicar a Lei de Ohm em e .
e
Mas o que é e ?
é a tensão em , então podemos dizer que é , Dessa forma ... Vamos organizar isso:
e
Substituindo:
e
Já sabemos que , então podemos igualar ambas as equações.
Chegamos então:
.
Resposta
.
.
Exercícios de Livros Relacionados
Deduza a Equação 5.60.
O sinal v g no circuito mostrado na Figura P5.36 é descrito pelas seguintes equações: v g=0 ,t ≤0 , v g=4c o s π 4 tV ,0 ≤t ≤ ∞ . Desenhe um gráfico de vo versus t, supondo que o amp op seja ideal
Suponha que o amp op ideal no circuito da Figura P5.40 esteja operando em sua região linear. a) Calcule a potência fornecida ao resistor de 16 kV.b) Repita (a) retirando o amp op do circuito, isto é,
Os amp ops no circuito da Figura P5.41 são ideais. a) Determine i a . b) Determine o valor da tensão da fonte à esquerda, para a qual i a = 0 .
A tensão v g mostrada na Figura P5.35(a) é aplicada ao amplificador inversor da Figura P5.35(b). Desenhe um gráfico de vo versus t, supondo que o amp op seja ideal