Não há nenhuma energia armazenada no circuito da Figura P13.83 no instante em que a tensão impulsiva é aplicada.
a) Determine vo, t para t 0.
b) Sua solução faz sentido em termos do comportamento conhecido do circuito? Explique.
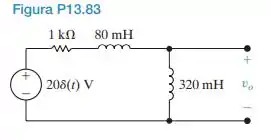
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre a transformada de Laplace na análise de circuitos!
- Analisando o circuito acima, temos:
- No momento nosso circuito é:
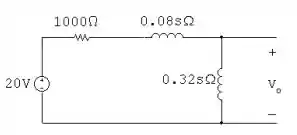
Desse circuito, podemos tirar a seguinte relação:
Portanto:
Passo 2
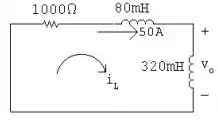
Ou seja:
Uma vez que:
Logo:
Portanto:
O que faz sentido com nossa solução.
Resposta
- Item a:
- Item b: Sim.
Então é isso, pessoal! Nos vemos na próxima questão. 😊