Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 16.Problemas - Ex. 18
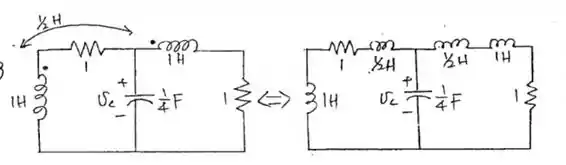
Note que, para bobinas acopladas, podemos sempre escolher as atribuições de corrente entrando nos pontos e as polaridades positivas das tensões nos pontos, como na Fig. 16.3(a). (Isso, certamente, pode requerer o uso de no lugar de etc.) Mostre que, se resolvermos as equaçóes representativas (16.16) para as derivadas da corrente e integrarmos o resultado, teremos
onde é o determinante
Este resultado nos possibilita resolver circuitos acoplados com análise nodal.
Passo 1
Note que, para bobinas acopladas, podemos sempre escolher as atribuições de corrente entrando nos pontos e as polaridades positivas das tensões nos pontos, como na Fig. 16.3(a). (Isso, certamente, pode requerer o uso de no lugar de etc.) Mostre que, se resolvermos as equaçóes representativas (16.16) para as derivadas da corrente e integrarmos o resultado, teremos
