Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 81
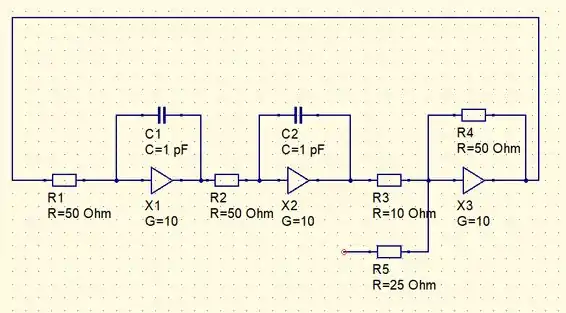
Projete um computador analógico para simular a seguinte equação:
Passo 1
Para projetar um circuito que simule a equação diferencial dada vamos precisar de um módulo para executar a derivada segunda, um módulo para executar a multiplicação por um escalar e um módulo que concatene todos esses resultados com uma soma/subtração. Assim, vamos pegar nossa equação diferencial dada e reescrevê-la como sendo
Dessa forma, podemos implementar o seguinte circuito
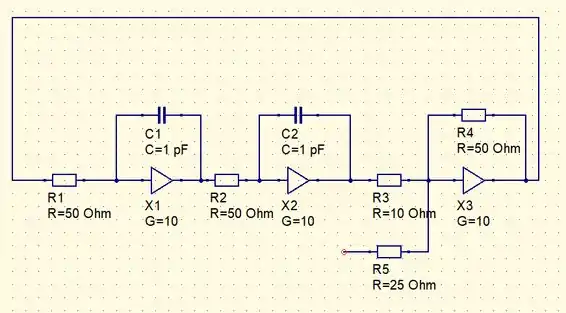
Resposta
Exercícios de Livros Relacionados
A figura 6.93 apresenta um computador analógico projetado para solucionar uma equação diferencial. Supondo que f t seja conhecida, monte uma equação para f t .
Projete um circuito com amplificador operacional tal que v 0 = 10 ⋅ v s + 2 ⋅ ∫ v s d t Onde v s e v 0 são, respectivamente, a tensão de entrada e a de saída.
Um circuito R C possui R = 2 Ω e C = 4F . A constante de tempo é: a0,5s b2s c4s d8s e15s
Um capacitor em um circuito R C com R = 2 Ω e C = 4F está sendo carregado. O tempo necessário para a tensão no capacitor atingir 63,2 % de seu valor em regime estacionário é: a2s b4s c8s d16s en e n h
Determine a constante de tempo para o circuito R C da figura 7.82.