Determine a constante de tempo para o circuito da figura 7.82.
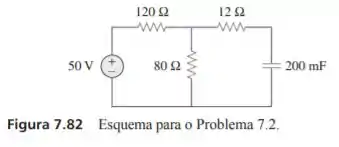
Passo 1
Para um circuito temos que a constante de tempo é dada por , porém, essa resistência é a resistência Thevenin para esse circuito. Então, vamos calcular primeiramente o valor dessa resistência para depois encontrarmos a constante de tempo
Agora, para concluirmos o exercício basta fazermos