Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 80
A figura 6.93 apresenta um computador analógico projetado para solucionar uma equação diferencial. Supondo que seja conhecida, monte uma equação para .
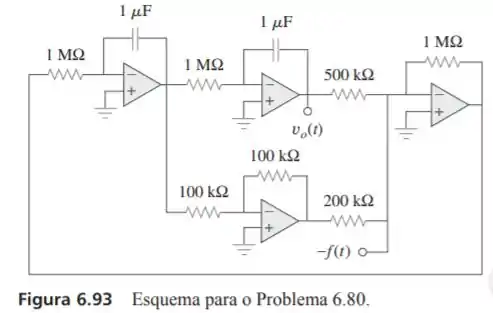
Passo 1
Utilizando a lei dos nós para esse circuito, lembrando-se do que cada parte que contém um amplificador operacional sozinho faz (diferencia, subtrai...) podemos equacionar o seguinte
Resposta
Exercícios de Livros Relacionados
Supondo que a chave na figura 7.87 se encontra na posição A há um longo período e seja mudada para a posição B em t = 0 . Em seguida, tem t = 1s , a chave se move de B para C . Determine v c t para t
Usando a figura 7.85, elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos R C sem fontes.
A chave da figura 7.86 foi fechada há um bom tempo e é aberta em t = 0 . Determine v t para t ≥ 0 .
Determine a constante de tempo para o circuito da figura 7.83.
Para o circuito da figura 7.88, se v = 10 ⋅ e - 4 tVei = 0.2 ⋅ e - 4 t , t0 a Determine R e C . b Determine a constante de tempo. c Calcule a energia inicial no capacitor. d Obtenha o tempo necessário