Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 80
Refaça o problema usando o PSpice ou MultiSim.
Passo 1
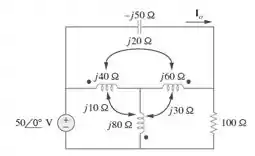
Bom, galerinha, vamos usar o PSpice para resolver essa questão, beleza? Primeiro de tudo, vamos transformar os elementos do circuito do domínio da frequência para o domínio da tempo. Considerando :
Além disso, vamos calcular os coeficientes de acoplamento:
Feito isso, podemos montar nosso circuito no software:
Passo 2
No prgrama, nós escolhemos AC Sweep no menu Analysis/Setup. Colocamos Total Pts igual a , Start Freq em e End Freq em .
Após simular o circuito, o arquivo de saída irá conter a frequência da fonte e os atributos escolhidos para o pseudocomponente (IPRINT). Assim, para a corrente :
Escrevendo em termos de fasor:
Resposta
As correntes são iguais a:
Exercícios de Livros Relacionados
Use o PSpice ou MultiSim para determinar I 1 , I 2 e I 3 no circuito da Figura 13.142 .
Determine I X e V X no circuito da Figura 13.144 usando o PSpice ou MultiSim
Use o PSpice ou MultiSim para determinar V 1 , V 2 e I 0 no circuito da Figura 13.14 3 .
Determine I 1 , I 2 e I 3 no circuito do transformador ideal da Figura 13.14 5 usando o PSpice ou MultiSim
Como mostra a perspectiva prática, o projeto de autocapacitância não permite uma verdadeira tela de múltiplos toques – se a tela é tocada em dois pontos, quatro locais de contato são identificados: do