Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 37
Refaça o Problema 14.25 para o caso no qual os elementos estejam ligados em paralelo.
Problema 14.25
14.25 Um circuito em série tem , e . Calcule a impedância na ressonância para frequências de um quarto, a metade, o dobro e de quatro vezes a frequência de ressonância.
Passo 1
Essa é uma questão desafiadora, o maior trabalho está no desenvolvimento matemático, mas juntos vamos resolver =).
Primeiro vamos analisar o circuito com os elementos em paralelo como a questão pede:
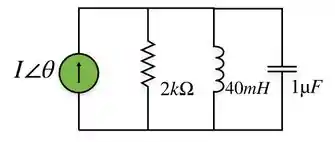
Você já deve saber, que estamos analisando um circuito com corrente alternada, por isso, vamos converte-lo com técnicas matemáticas, para que ele se “pareça com um circuito continuo”, que são muito mais simples de calcular. Aplicamos o fator para isso. O circuito ficará assim:
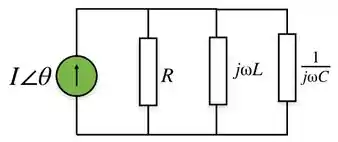
Veja que até desenhamos os componentes de outra maneira, para te passar a ideia de que agora podemos tratar esse circuito como um circuito contínuo. Tanto , são vistos como impedâncias agora. Vamos chamá-los e então fazer o paralelo dos componentes para achar uma impedância em cada caso na ressonância como pede a questão.
Passo 2
Vamos ver como podemos calcular a impedância .
A fórmula de impedância em paralelo é:
Substituindo os termos:
Simplificando:
A unidade imaginaria , possui uma identidade especial que diz que:
Então vamos com isso pôr o em evidência e continuar simplificando, observe como:
Agora vamos Isolar :
Finalmente:
No fundo o que estamos fazendo é achar a admitância , que é aparte debaixo da fórmula entre colchetes , e pelo inverso acharemos a impedância . Estamos trabalhando com números complexos, então é importante o uso de uma calculadora científica!
Passo 3
Agora que temos uma expressão para achar . vamos determinar a frequência de ressonância , que funciona como uma espécie de barema, usaremos a fórmula geral de um em paralelo :
Agora usaremos a igualdade do meio:
Substituindo os valores:
Passo 4
Agora que temos a expressão de e o valor da frequência de ressonância acharemos a impedância em cada caso solicitado na questão, substituindo os valores:
um quarto de
A metade de
O dobro de
Quatro vezes de
Resposta
Um quarto de
A metade de
O dobro de
Quatro vezes de