Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 2.Problemas - Ex. 23

O resistor variável R no circuito da Figura P2.23 é ajustado até que i 0 seja igual a 10 mA. Determine o valor de R.

Passo 1

Iae, meus queridos! Td certinho??

Muito legal esse tipo de questão, minha sugestão é resolver por analise de malhas.

Analisando o circuito, temos que temos 3 malhas, portanto vamos desenvolver as equações.

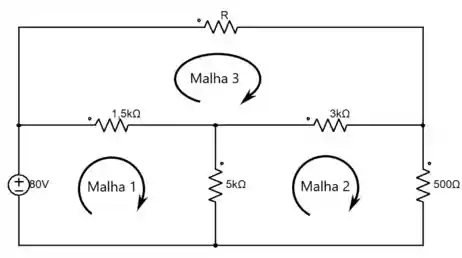
Malha 1:

80 = 1,5 k i 1 - i 3 + 5 k i 1 - i 2

6,5 k i 1 - 5 k i 2 - 1,5 k i 3 = 80

Malha 2:

500 i 2 + 5 k i 2 - i 1 + 3 k i 2 - i 3 = 0

- 5 k i 1 + 8,5 k i 2 - 3 k i 3 = 0

Malha 3:

R i 3 + 1,5 k i 3 - i 1 + 3 k i 3 - i 2 = 0

- 1,5 k i 1 - 3 k i 2 + 4,5 k + R i 3 = 0

Juntando tudo, temos

6,5 k i 1 - 5 k i 2 - 1,5 k i 3 = 80 - 5 k i 1 + 8,5 k i 2 - 3 k i 3 = 0 - 1,5 k i 1 - 3 k i 2 + 4,5 k + R i 3 = 0

Passo 2

Resolvendo o sistema acima, a partir dos inúmeros métodos de soluções, chegamos no seguinte resultado.

i 1 = 2139280 R + 7361640000 786500 121 R + 54 k i 2 = 96,8 k R + 522720000 60,5 k 121 R + 54 k i 3 = 8880 121 R + 54 k

A partir da referencia que usamos para analisar o sentido das correntes, vemos que

i 0 = i 1 - i 2

Ou seja

i 0 = 2139280 R + 7361640000 786500 121 R + 54 k - 96,8 k R + 522720000 60,5 k 121 R + 54 k

Se i 0 = 10 m A , então

2139280 R + 7361640000 786500 121 R + 54 k - 96,8 k R + 522720000 60,5 k 121 R + 54 k = 10 m

2139280 R + 7361640000 786500 - 96,8 k R + 522720000 60,5 k = 10 m 121 R + 54 k

2,72 R + 9360 - 1,6 R + 8640 = 1 , 21 R + 540

- 0,09 R = - 180

R = 2 k Ω .

achou tranquilo? Bora praticar mais! 😎

Resposta

R = 2 k Ω .

Exercícios de Livros Relacionados

No circuito da figura 2.75 , determine V_1 e V_2 .
Determine i_1 e i_3 no circuito da figura 2.74 .
As correntes i a e i b no circuito da Figura P2.26 são 4 A e -2 A, respectivamente. a) Determine i g. b) Determine a potência dissipada em cada resistor. c) Determine vg. d) Mostre que a potência forn
Para o circuito mostrado na Figura P2.36, calcule i ∆ e v σ e (b) mostre que a potência fornecida é igual à potência absorvida.
Para o circuito mostrado na Figura 2.24, R1 = 40 kV, R2 = 60 kV, RC = 750 V, RE = 120 V, VCC = 10 V, V0 = 600 mV e β = 49. Calcule iB, iC, iE, v3d, vbd, i2, i1, vab, iCC e v13. (Observação: na notação