Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 89

O resistor variável no circuito da Figura P4.89 é ajustado para a máxima transferência de potência para R o .

a) Determine o valor de R o .

b) Determine a potência máxima fornecida a Ro.

c) Qual é a potência que a fonte de 180   V fornece ao circuito, quando Ro é ajustado para o valor calculado em ( a ) ?

Passo 1

Okaaay turminha, bora lá! Primeiro encontraremos o equivalente de Thévenin em relação a Ro.

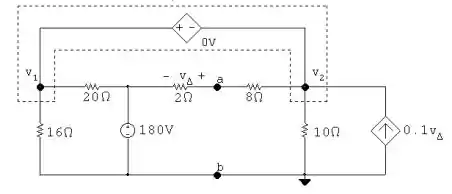
Buscando os nós:

v 1 16 + v 1 - 180 20 + v 1 - 180 10 + v 1 10 - 0.1 v Δ = 0

v Δ = v 1 - 180 10 2 = 0.2 v 1 - 36

v 1 = 80 V ;     v Δ = - 20 V

Logo,

V t h = 180 + v Δ = 180 - 20 = 160   V

Passo 2

A partir disso, podemos ter a corrente de curto circuito da seguinte forma:

v 1 16 + v 1 - 180 20 + v 2 8 - 0.1 - 180 = 0

v 2 + 184 i ϕ = v 1

i ϕ = 180 2 + v 2 8 = 90 + 0.125 v 2  

v 2 = - 640 V ;     v 1 = 1200   V

Jogando isso na equação, temos:

i ϕ = i s c = 10 A

R t h = V t h i s c = 160 10 = 16   Ω

R 0 = 16   Ω

Passo 3

Agora passando pro item b), é bem tranquilo, temos:

Logo,

p m a x = 80 2 16 = 400   W

Passo 4

Por fim, no item c), temos:

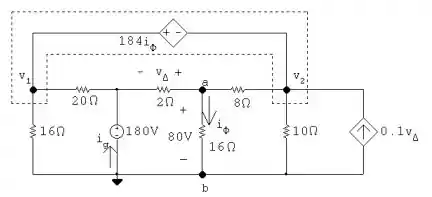
Pegando a equação dos nós:

v 1 1 6   +   v 1   -   180 20 + v 2 - 80 8   + v 2 10 -   0.1 ( 80   -   180 )   =   0

v 2 + 184 i ϕ = v 1 ;     i ϕ = 80 16 = 5 A

Sabendo das tensões,

v 1 = 640   V   e   v 2 = 280   V

Logo,

i g = 180 - 80 2 + 180 - 640 20 = 27 A

Portanto,

p 180 v d e v = 180 27 = 4860   W

Resposta

a ) R o = 16   Ω

b ) p m a x = 400   W

c ) p 180 v = 4860   W

Exercícios de Livros Relacionados

Calcule o equivalente de Norton, do circuito à esquerda dos terminais a - b , e use o resultado para calcular i .
Calcule o equivalente de Norton, do circuito à esquerda dos terminais a ⋅ b , e use o resultado para calcular v .
Substitua o circuito à esquerda dos terminais a - b pelo seu equivalente de Thévenin e use o resultado para calcular v .
Calcule o equivalente de Jhivenin do circuito externo ao resistor de 4 Ω e use o resultado para encontrar i.
Obtenha o equivalente de Norton em relação aos terminais a, b para o circuito da Figura P4.68.