Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 44

Resolva o Problema 4.13 usando o método das correntes de malha.

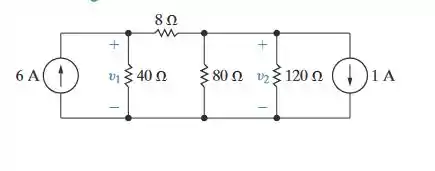
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Primeiramente, vamos aplicar o método das correntes de malha na segunda malha, com isso, nós temos que:

40 i 1 - 6 + 8 i 1 + 80 i 1 - i 2 = 0

Aplicando a propriedade associativa, nós temos que

128 i 1 - 80 i 2 = 240               ( 1 )

Já na malha 3, nós obtemos o seguinte resultado:

80 i 2 - i 1 + 120 i 2 - 1 = 0  

Desenvolvendo um pouco mais,

200 i 2 - 80 i 1 = 120     2

Fazendo o sistema de equações e resolvendo (1) e (2)

i 1 = 3   A

i 2 = 1,8   A

Passo 2

Agora, nós vamos calcular o valor de V 1 :

V 1 = 40 6 - i 1

Desenvolvendo

V 1 = 40 6 - 3 = 120   V

Logo, nós temos que V 1 é igual a

V 1 = 120   V

Passo 3

Calculando o V 2 , nós obtemos o seguinte resultado

V 2 = 120 i 2 - 1

Desenvolvendo o termo, nós temos que

V 2 = 120 1,8 - 1 = 96   V

Resposta

V 1 = 120   V

V 2 = 96   V

Exercícios de Livros Relacionados

Calcule i.
Calcule v.
Calcule i e a resistência vista pela fonte independente de corrente se (a) R = 6 Ω e (b) R = 1 Ω.
(a) Na Figura do Prob. 3.14. considere que R 0 = 10 k Ω e encontre R 1 e R 2 tal que o módulo da tensão de saída v 3 seja a media dos valores das tensões de entrada v 1 e v 2 . (b) Calcule R 1 se R 0
Resolva o Prob. 2.38, usando a propriedade da proporcionalidade.