Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 43
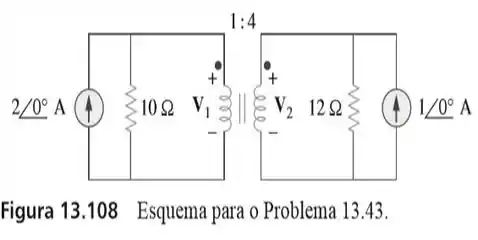
43. Obtenha e no circuito do transformador ideal da Figura 13.108.
Passo 1
Olha só! No circuito da figura do enunciado, temos uma coisa interessantes. Uma fonte de corrente em paralelo com uma resistência, tanto do lado esquerdo como direito.
E sabe o que isso, quer dizer!?
Quer dizer que podemos usar a transformação de fontes. Isso é, transformar a associação em paralelo entre a fonte de corrente e a resistência, em uma associação em série entre a mesma resistência e uma fonte de tensão.
Desse modo, vamos calcular o quanto valem essas fontes de tensão...
E depois, vamos redesenhar esse circuito com essas transformações. Aproveitando a deixa, bora deixar indicado também, as correntes de malha.
Passo 2
Aqui está...
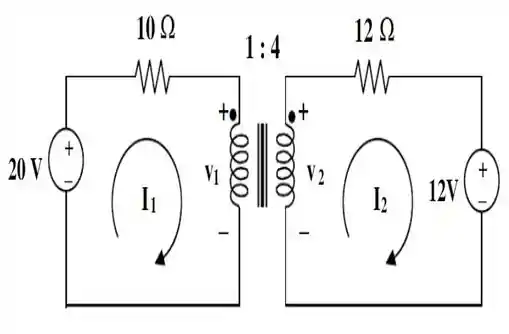
Aplicando a para a malha :
E depois, aplicando a para a malha :
Ih rapaz! Tem variáveis nessas duas equações aí...
Será que tem um jeito de reduzir esse número!?
Pois é. A resposta é sim! Lembra lá das relações de tensão e corrente no transformador. Pois bem, olhando a figura podemos ver que:
E como a relação entre as corrente é inversamente proporcional a isso...
Substituindo essas duas igualdades anteriores em ...
Passo 3
Ficamos então, com o seguinte sistema pra resolver...
Multiplicando por ...
E depois somando as duas equações, obtemos que:
A tensão , por sua vez, é dada por:
E do , sabemos que...
Sendo assim,
Finished!