Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 46

Passo 1

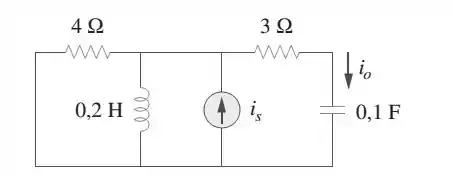
Dado que i_s = 5 < 40 º A e omega = 10 r a d // s

Vemos que a as impedâncias do lado esquerdo da fonte de corrente ( 4 omega e 0,2 H estão em paralelo:

Z_1 = (4 (j xx 10 xx 0,2))/(4 + j xx 10 xx 0,2) (j 8)/(4 + j 2) = (j 8 (4 - j 2))/(20) = (16 + j 32)/(20) Z_1 = ( 0,8 + j 1,6 )

Para o lado direito do circuito, as impedâncias de 3 omega e 0,1 F estão em série:

Z_2 = 3 + (1)/(j xx 10 xx 0,1) Z_2 = (3 - j) omega

Passo 2

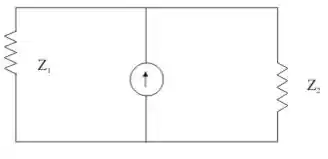
O circuito equivalente se torna:

Passo 3

Agora, por divisor de corrente, temos:

I_0 = ((Z_1)/(Z_1 + Z_2)) I_s I_0 = (0,8 + j 1,6)/(0,8 + j 1,6 + 3 - j) xx (5 < 40 º) I_0 = ((0,8 + j 1,6)/(3,8 + j 0,6)) (5 < 40 º) I_0 = ((1,789 < 63,43 º)/(3,387 < 8,97 º)) xx (5 < 40 º) I_o = 2,325 < 94,46 º A

No domínio do tempo:

i_0 = 2,325 cos (10 t + 94,46) A

Resposta

i_0 = 2,325 cos (10 t + 94,46 º)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura 9.54, determine o valor de i_s (t) .
Determine a corrente I_0 no circuito da Figura 9.52:
Calcule i (t) no circuito da Figura 9.51.
Dado que v_s (t) = 20 sen (100 t - 40 º) º na Figura 9.55, determine i_x ( t ) :
Determine a admitância Y para o circuito da figura 9.44 .