Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 45

Determine a corrente I_0 no circuito da Figura 9.52:

Passo 1

Redesenhando o circuito e nomeando as correntes em cada ramo:

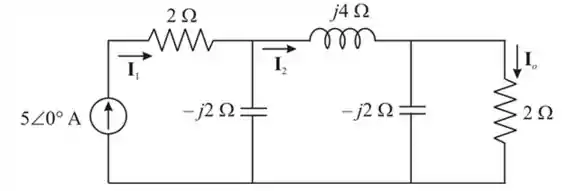
Passo 2

Do circuito acima:

I_1 = 5 < 0 º A

O resistor de 2 omega e o resistor e a impedância de - j 2 omega estão em paralelo. A impedância equivalente é:

Z_e q_1 = 2 | | - j 2 = ([(2) xx (- j 2)])/(2 - j 2) = - (j 2)/(1 - j 1) = - j 2 (0,5 + 0,5 j) = Z_e q_1 = 1 - j 1 omega

Passo 3

Redesenhando o circuito:

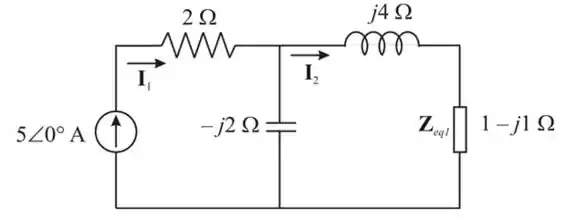
Aplicando a expressão do divisor de corrente: I_2 = [(- j 2)/(- j 2 + j 4 + 1 - j 1)] (I_1) = [- (j 2)/(- j 2 + j 4 + 1 - j 1)] (5 < 0 º) = [- (j 2)/(1 + j 1)] xx (5 < 0 º) I_2 = 7,072 < - 135 º A

Passo 4

Aplicanto a divisão de corrente no circuito:

I_0 = [- (j 2)/(- j 2 + 2)] (I_2) = [- (j 1)/(- j 1 + 1)] xx (7,072 < - 135 º) = [(1 < - 90 º)/(1,414 < - 45 º)] (7,072 < - 135 º) = - 5 A

Resposta

I_0 = - 5 A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando a figura 9.43 , elabore um problema para ajudar outros estudantes a entenderem melhor a impedância.
No circuito da Figura 9.47 , determine i 0 quando: ω = 1r a d / s ; ω = 5r a d / s ; ω = 10r a d / s .
50- Determine v x no circuito da Figura 9.57 . Considere i s t = 5 cos ⁡ 100 t + 40 ° A
56- Com ω = 377r a d / s , determine a impedância de entrado do circuito mostrado na Figura 9.63 .
52- Se V o = 8 ∠ 30 °V no circuito da Figura 9.59 , determine I s .