Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 48

Dado que v_s (t) = 20 sen (100 t - 40 º) na Figura 9.55, determine i_x ( t ) :

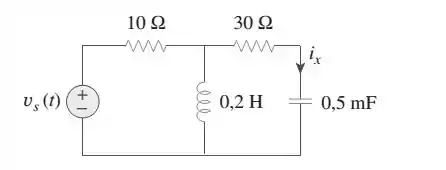
Passo 1

A tensão da fonte é v_s = 20 sen (100 t - 40 º) V

Sabe-se que:

sen (theta) = cos (theta - 90 º)

Convertendo a tensão da fonte para a forma de cosseno:

v_s (t) = 20 cos (100 t - 40 º - 90 º) V = 20 cos (100 t - 130 º) V

A forma fasorial é:

V_s = 20 < - 130 º V

Passo 2

Da tensão fonte de tensão, a frequência angular é:

omega = 100 r a d // s

Calcule a impedância de 0,5 m F do capacitor:

- j X_C = (1)/(j omega c) = (1)/(j (100) (0,5 xx 10^(- 3))) = - j 20 omega

Passo 3

Desenhando o circuito no domínio da frequência:

Caculando a impedância equivalente vista da fonte:

Z_e q q = 10 + [ ( j j 20 ) | |(30 - j 20)] = 10 + (((j 20) (30 - j 20))/(j 20 + 30 - j 20)) = 10 + (400 + j 600)/(30) = 10 + 13,33 + j 20 = 23,33 + j 20 omega = 30,73 < 40,6 º omega

Passo 4

Calculando a corrente total fluindo da fonte:

I_t = (V_s)/(Z_e q) = (20 < - 130 º V)/(30,73 < 40,6 º omega) = 0,65 < - 170,6 º A

Passo 5

Agora, calculando a corrente I_x usando o divisor de corrente:

I_x = ((j 20)/(j 20 + 30 - j 20)) I_t ((j 20)/(30)) (0,65 < - 170,6) = (0,667 < 90 º) (0,65 < - 170,6 º) = 0,433 < - 80,6 º A

A corrente i_x no domínio do tempo é:

i_x (t) = 0,433 cos (100 t - 80,6 º) A

Resposta

i_x (t) = 0,433 cos (100 t - 80,6 º) A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

58- Usando a Figura 9.65 , elabore um problema para ajudar outros estudantes a entender melhor as associações e impedâncias:
60- Obtenha Z e n t para o circuito da Figura 9.67
61- Determine Z e q no circuito da Figura 9.68 .
59- Para o circuito da Figura 9.66 , determine Z e n t . Considere ω = 10r a d / s
65- Determine Z T e I no circuito da Figura 9.72 .