Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 44

Calcule i (t) no circuito da Figura 9.51.

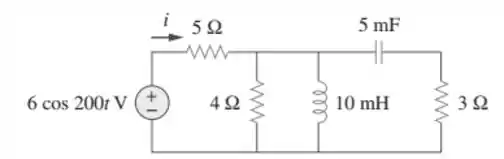
Passo 1

Observando o circuito, a tensão da fonte é v(t)=6cos(200t) V.

Da tensão da fonte, a frequência angular é omega = 200 r a d // s

Convertendo a tensão da fonte para a forma fasorial:

V = 6 < 0 º V

Passo 2

Convertendo a tensão da fonte para a forma fasorial:

V = 6 < 0 º V

Calculando a impedância de 10 m H do indutor.

Z_L = j omega L = j (200) (10 xx 10^(- 3)) = j 2 omega

Calculando a impedância de 5 m F do capacitor.

Z_c = (1)/(j omega C) = (1)/(j (200) (5 xx 10^(- 3))) = - j 1 omega

Passo 3

Desenhando o circuito no domínio da frequência:

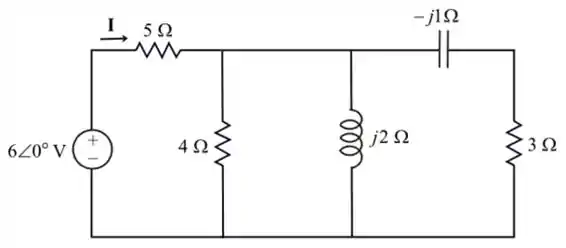
Na figura, a combinação série da resistência de 3 omega e do capacitor - j 1 omega está conectada em paralelo com o indutor de j 2 omega .

Calculando a impedância equivalente:

Z_e q_1 = (3 - j 1) | | ( j 2 ) = ((3 - J 1) (j 2))/((3 - j 1) + (j 2)) = (2 + j 6)/(3 + j) = 1,2 + j 1,6 omega

Passo 4

Da figura, calculamos a impedância total:

Z_t o t a l = [ ( Z_e q_1 ) | | + 5 = [((1,2 + j 1,6) (4))/(1,2 + j 1,6)] + 5 = 1,189 + j 0,865 + 5 = 6,25 < 7,95 º omega

Passo 5

Calculando a corrente que flui no circuito:

I = (V)/(Z_t o t a l) = (6 < 0 º)/(6,25 < 7,95 º) = 0,96 < - 7,95 A

Passo 6

Calculando no domínio do tempo:

i (t) = 0,96 cos (200 t - 7,95 º) A

Resposta

i(t)=0,96cos (200 t - 7,95 º)A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

57- Com ω = 1r a d / s , obtenha a impedância de entrada do circuito da Figura 9.64
55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V
51- Se a tensão v o no resistor de 2Ω no circuito da Figura 9.58 for 10 cos ⁡ 2 tV , obtenha i s :
54- No circuito da Figura 9.61 , determine V_s se I_o = 2 /_ 0 ° A .
49- Determine v s ( t ) no circuito da Figura 9.56 se a corrente i x no resistor de 1 Ω for 0.5s e n200 tA .