Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 7
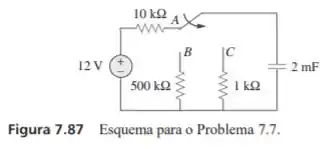
Supondo que a chave na figura 7.87 se encontra na posição há um longo período e seja mudada para a posição em . Em seguida, tem , a chave se move de para . Determine para .
Passo 1
Avaliando primeiramente quando a chave está na posição . Como o circuito se encontra dessa forma há muito tempo, o capacitor vai funcionar como um circuito aberto:
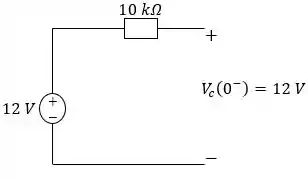
Como é um circuito aberto, não teremos corrente passando nele e, com isso, podemos dizer que a tensão em cima do capacitor será a mesma da fonte. Beleza? Guarda essa informação!
Passo 2
Em , a chave muda de para . E o nosso circuito passa a ser:
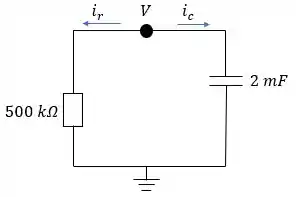
Então, já analisando nosso único nó desenhado ali, temos duas correntes saindo dele e indo para o terra, nosso nó de referência. Dessa forma:
Só que sabemos que a corrente no capacitor é e a corrente no resistor será . Logo:
Dividindo tudo por :
Agora, vamos resolver essa EDO para achar a tensão no capacitor para . Resolvendo essa EDO, temos a equação característica:
E nossa solução é:
Onde podemos achar o valor da constante usando a informação de que e sabendo que a tensão no capacitor não pode variar instantaneamente. Assim:
E:
Nossa solução, então, fica:
Passo 3
Agora, só falta analisar o circuito para . Nesse instante, a chave vai para e o nosso circuito fica assim:
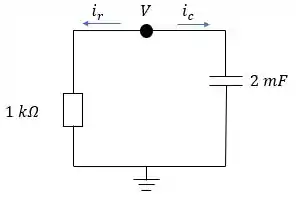
É bem parecido com o anterior mesmo! E vamos resolver da mesma forma, também. Então, já podemos montar nossa EDO pela análise nodal:
Só que sabemos que a corrente no capacitor é e a corrente no resistor será . Logo:
Dividindo tudo por :
Agora, vamos resolver essa EDO para achar a tensão no capacitor para . Resolvendo essa EDO, temos a equação característica:
E nossa solução é:
Por que e não ? Porque já se passou 1 segundo, então o instante inicial desse circuito é deslocado em 1s. Beleza?
E podemos achar o valor da constante usando a informação do passo anterior de que e sabendo que a tensão no capacitor não pode variar instantaneamente. Assim:
E:
Nossa solução, então, fica:
Passo 4
Para finalizar, precisamos só juntar todas as informações dos dois passos anteriores e chegar na resposta final:
Beleza?? Acabamos por aqui! 😊