Suponha que a tensao no Prob. 1.19 varie linearmente de a enquanto o tempo varia de a . Se durante esse tempo, calcule (a) a energia total fornecida e (b) a carga total entregue a bateria.
Passo 1
Falaaaa, galeraaaa! Vamos analisar o gráfico e utilizar:
- Da fórmula de potência: ;
- Da equação fundamental da reta: ;
- Da relação entre potência e energia: ;
- Da relação entre corrente e carga: .
Passo 2
O gráfico que representa o problema exposto é mostrado abaixo. Observe que o eixo do tempo está em segundos, logo o valor de passou a ser .
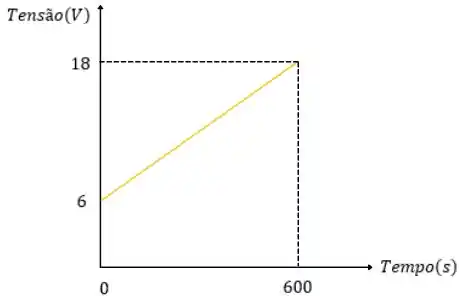
Primeiro, com base no gráfico devemos obter a inclinação da reta.
Temos que:
Isolando:
A equação da reta será então:
Passo 3
Letra a):
Para calcular a energia devemos obter a expressão da potência antes de tudo. Dessa forma
A energia então será
Substituindo em :
Integrando temos
Passo 4
Letra b):
Vamos calcula a carga por meio da seguinte expressão:
Integrando
Prontinho!

Resposta
a.
b.