Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas Abrangentes - Ex. 80

80. Um alto-falante é conectado a um amplificador, conforme mostrado na figura 2.139 . Se um de 10   Ω consumir uma potência máxima de 12   W do amplificador, determine a potência máxima que um alto-falante de 4   Ω consumirá.

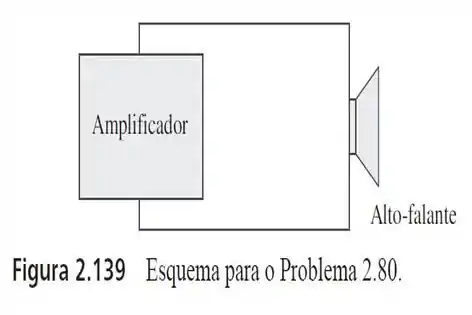
Passo 1

Bom! A potência é dada em função da voltagem e da resistência, pela seguinte fórmula:

P = V 2 R

Então, considerando que o amplificador é o mesmo para os dois casos e portanto tem a mesma voltagem, obtemos que:

V 2 = P R

Ou seja, a relação P R é constante. Desse modo, basta fazer assim...

P 1 R 1 = P 2 R 2

Onde P 1 = 12   W , R 1 = 10   Ω , R 2 = 4   Ω e P 2 ... Bem! P 2 é o que nós queremos determinar:

P 1 R 1 = P 2 R 2

P 2 = P 1 R 1 R 2

P 2 = 12   W ⋅ ( 10   Ω ) 4   Ω

P 2 = 30   W

Resposta

P o t ê n c i a   c o n s u m i d a → P 2 = 30   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a potência máxima que pode ser entregue ao resistor R e o valor de R para a potência máxima no circuito do Prob 5.27.
Calcule o valor de R que irá retirar a potência máxima do restante do circuito. Calcule também a potência máxima.
Calcule a potência máxima que pode ser entregue a R se (a) R 1 = 12 Ω e (b) R 2 = 30 Ω .
Calcule a potência entregue a um elemento em t=2m s se a carga que entra pelo terminal positivo é q=12 cos ⁡ 125 π tm C e a tensão é v=4 sen ⁡ 125 π tV
Calcule 0 valor de R que irá consumir a potência máxima do resto do circuito. Calcule também a potência máxima consumida por R.