Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 19

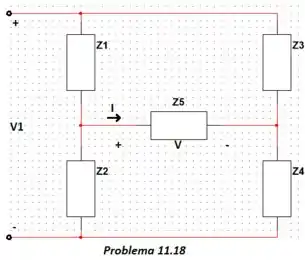
Mostre que o circuito do Prob. 11.13 é uma ponte equilibrada com associação série de 2   Ω e 1 2   H , constituindo Z 5 no Prob. 11.18. Substitua Z 5 por um curto e mostre que o mesmo v é obtido como antes.

Passo 1

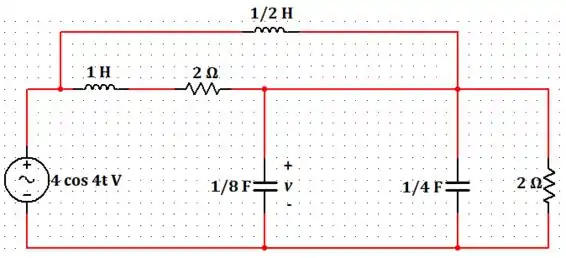
Vaalha misturaram duas questões aqui, viiixe. Calma, calma, calma. Olha, basicamente só precisamos trocar a associação série de 2   Ω e 1 2   H da figura da questão 13 por um curto circuito. Dessa forma, temos:

Passo 2

Seguinte... Vamos primeiro passar os valores da fonte para a forma polar e enxergar os capacitores e os indutores em forma de reatâncias.

Lembrando que:

X C =   - j ω C

X L = j ω L

Em que ω = 4   r a d / s .

Logo, temos:

Passo 3

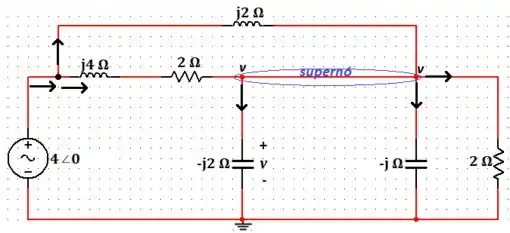
Agora, vamos selecionar os seguintes nós e atribuir direções da corrente e também vamos colocar o terra (referencial de potencial 0 V) na parte de baixo do circuito para facilitar nossa vida hehe:

Passo 4

Aí, utilizando a Lei dos Kirchhoff das Correntes no supernó, temos:

4 - v 2 + j 4 + 4 - v j 2 = v - j 2 + v - j + v 2 ∴

4 - v 2 + j 4 - j 4 - j v 2 = v 1 + j 3 2 ∴

4 - v 2 + j 4 = j 3 v + v 2 + j 4 - j v 2 ∴

0.4 - j 0.8 - v 0.1 - j 0.2 = j 2 v + v + j 4 2 ∴

0.8 - j 1.6 - 0.2 v + j 0.4 v = j 2 v + v + j 4 ∴

v = 0.8 - j 5.6 1.2 + j 1 . 6 ∴

v = 2 2 ∠ - 135 ° V

Logo, como o valor é o mesmo encontrado na questão 13, então podemos concluir que trata-se de um circuito com ponte equilibrada!! Massa né?

Resposta

v = 2 2 cos ⁡ 4 t - 135 ° V

Exercícios de Livros Relacionados

a) A tensão da fonte no circuito da Figura P9.40 é vg = 40 cos 1.000t V. Determine os valores de L em que i g fica em fase com vg quando o circuito estiver em regime permanente. b) Para os valores de
A frequência da fonte de tensão no circuito na Figura P9.38 é ajustada até que vg fique em fase com i g. Qual é o valor de v em radianos por segundo? b) Se i g = 60 cos vt mA (onde v é a frequência de
O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
Use o método das tensões de nó para determinar a expressão de regime permanente para i o no circuito visto na Figura P9.56, se i g = 5 cos 2.500t A e vg = 20 cos (2.500t + 90º) V.
No circuito da Figura P9.67, suponha que v1 = 20 cos(2.000t - 36,87°) V, v2 = 10 cos(5.000t + 16,26°) V. a) Qual é a técnica de análise de circuitos que deve ser utilizada para determinar a expressão