Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 38
Suponha que o voltímetro de d’Arsonval descrito no Problema 3.37 seja usado para medir a tensão no resistor de da Figura P3.38.
a) Qual será a leitura do voltímetro?
b) Determine o erro percentual na leitura do voltímetro, se
Passo 1
Faaaaaaaaaala, pessoal! Vamos dar início a essa questão, mas pra entende-la, vamos precisar usar os conceitos que foram usados na questão anterior. Mas pra você não precisar voltar pra lá, vou resumir aqui
O circuito da questão 3.37 funciona como se fosse um multímetro. Para você usar um multímetro, você, por segurança, coloca na faixa de valores mais alta e gradativamente vai baixando até que a medição que você vai fazer esteja numa escala adequada. Pois bem, foram dadas 4 situações e para cada uma delas foram obtidos 4 valores diferentes para a resistência interna do voltímetro, . Isso significa que teremos que escolher uma que seja adequada ao circuito atual.
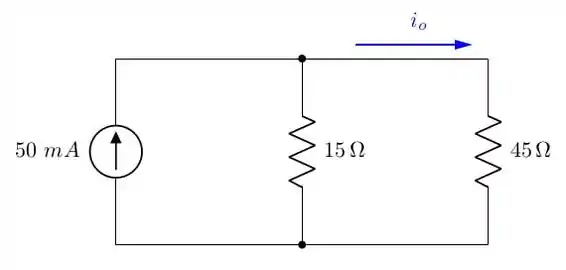
Para sabermos qual vai ser a faixa considerada, vamos usar um simples divisor de corrente no circuito abaixo e saber qual a corrente no resistor de :
Assim, a tensão neste resistor será:
Voltando à questão 3.37, veremos que a melhor escala a ser usada é a que mede uma tensão de , visto que as 2 inferiores não seriam suficientes para suportar a tensão no resistor, vindo a queimar o circuito de proteção do voltímetro. Além disso, a escala de poderia não fornecer uma precisão satisfatória, visto que o valor da tensão é muito baixo se comparado ao valor medido.
Passo 2
Uma vez que escolhemos qual o valor de , vamos acoplar o voltímetro ao circuito. O voltímetro será composto de 2 resistências: que já foi calculada na questão anterior, mas a resistência que é obtida através das indicações do voltímetro (e ). Estas duas resistências estarão em série. Para ficar melhor de compreender o que foi escrito, observe a figura abaixo:
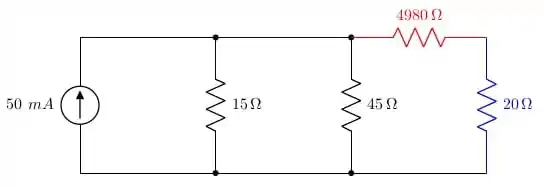
onde o resistor vermelho representa e o resistor azul representa o valor que foi obtido pela Lei de Ohm das indicações internas do voltímetro. Assim, basicamente teremos que analisar o seguinte circuito:
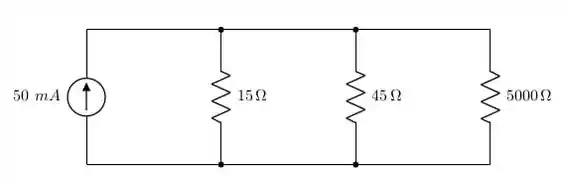
Perceba que todos os 3 resistores estão em paralelo. Assim, a tensão em 1 será a mesma em todos. Logo, pela Lei de Ohm, temos que encontrar a resistência equivalente em paralelo e multiplicar esta pela corrente da fonte. Então:
Passo 3
b)
Este item se torna bem mais simples porque já calculamos o valor real no item anterior. Tudo o que temos que fazer aqui é substituir os valores na equação dada:
E assim, finalizamos mais uma questão delicinha... Let’s bora!
Resposta
a)
b)