Conecte uma fonte de tensão de entre os terminais a-b na Figura P3.9 (b), com o terminal positivo na parte superior.
a) Use a divisão de tensão para determinar a tensão nos terminais do resistor de , positiva na parte superior.
b) Use o resultado de (a) para determinar a corrente no resistor de , da esquerda para a direita.
c) Use o resultado de (b) e a divisão de corrente para determinar a corrente no resistor de , da esquerda para a direita.
d) Use o resultado de (c) e a divisão de corrente para determinar a corrente no resistor de , de cima para baixo.
e) Use o resultado de (d) para determinar a tensão nos terminais do resistor de , positiva na parte superior.
f) Use o resultado de (e) e a divisão de tensão para determinar a tensão nos terminais do resistor de , positiva na parte superior.
Passo 1
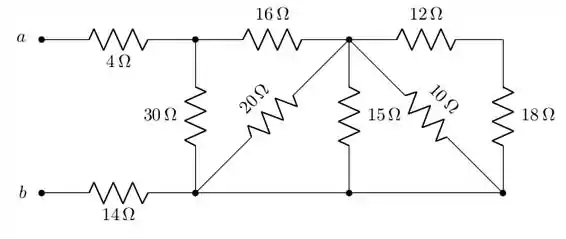
Show de bola, galera! Vamos começar, como é de praxe, mostrando qual é a figura que o livro está trabalhando:
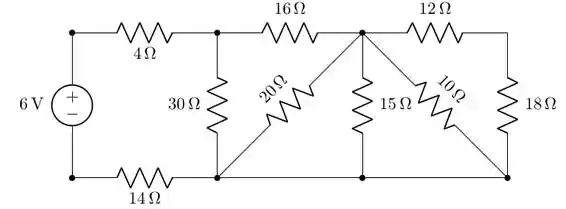
A questão pede para ligarmos uma fonte aos pontos a e b. Eis aqui a ligação:
Agora, vamos resolver o que se pede nos itens (a) a (f)
Passo 2
(a)
Essa será uma parte bem trabalhosa porque iremos simplificar o circuito da direita para a esquerda. Para isso, vamos fazer a simplificação passo a passo. Começaremos somando os resistores de e e fazendo esta associação série em paralelo com o resistor de :
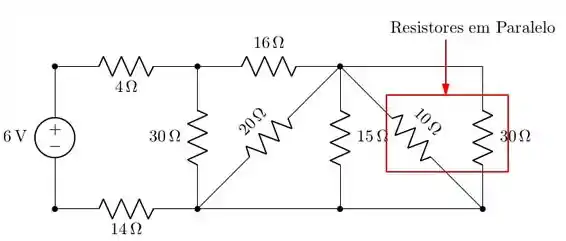
Essa primeira resistência equivalente será:
Redesenhando o circuito com essa nova informação, obtemos o seguinte:
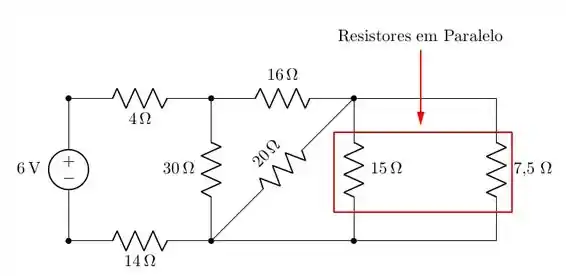
Essa imagem já nos dá uma pista do nosso próximo passo que será calcular a resistência em paralelo destacada:
Redesenhando o circuito, obtemos:
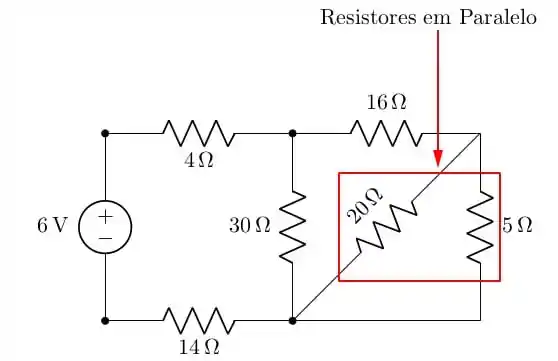
Calculando esta nova associação em paralelo, obtemos:
Esse resistor será somado ao de formando uma resistência de :
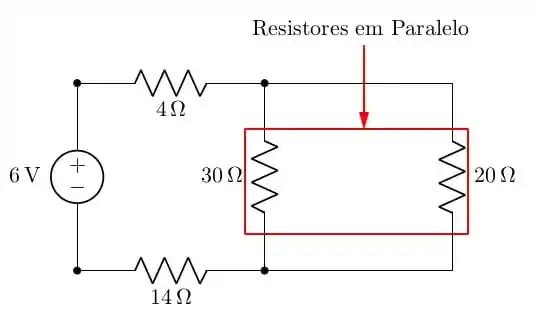
Na figura já há a indicação do que iremos calcular, e para a surpresa de 0 pessoas, será o cálculo de uma resistência equivalente em paralelo:
Finalmente, chegamos ao circuito necessário para fazer uso da técnica do divisor de tensão:
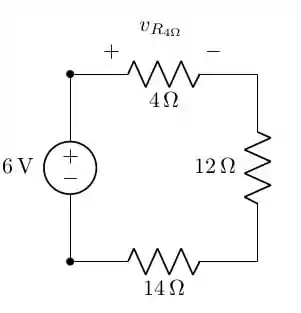
Assim, a tensão no resistor de será:
Passo 3
b)
A corrente no resistor será dada por:
Passo 4
c)
Para sabermos qual será o valor da corrente pedida, vamos ter que mostrar o circuito como estava imediatamente antes da simplificação. Se voltarmos um pouco, vamos ver que a associação deu um resistor de . Não mostramos o circuito, por isso iremos fazê-lo agora:
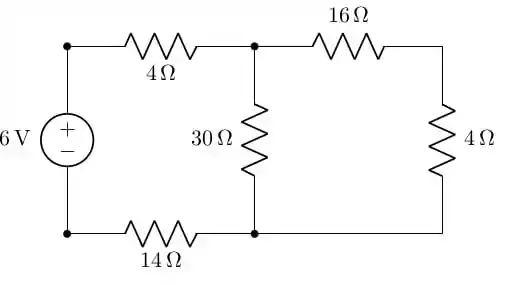
Assim, a corrente que passa no resistor de , ao lado da fonte de tensão, irá se dividir entre o resistor de e a associação cujo valor é de . Como a corrente num resistor em série e a mesma para cada elemento, a corrente no resistor equivalente de será a mesma nos resistores de e . Assim:
Passo 5
d) Observe a figura abaixo:
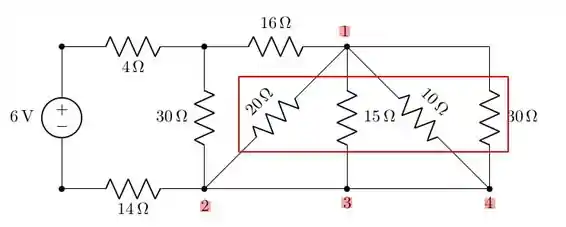
Observe que os 4 resistores destacados estão ligados ao ponto 1. Ao mesmo tempo que os pontos 2, 3 e 4 estão ligados e não há nenhum elemento entre eles. Isso significa que esses resistores estão ligados em paralelo. Sendo assim, podemos usar a divisão de corrente nesta situação, mas será preciso utilizar a equação genérica para a divisão de corrente:
Passo 6
e)
Essa fica fácil porque é só aplicar a Lei de Ohm:
Passo 7
f)
Para conseguirmos visualizar esse item, vamos voltar à figura original:
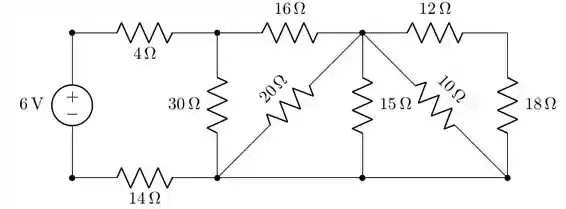
É possível perceber que o resistor de está em paralelo com a associação série dos resistores de e . Sabendo disso, podemos facilmente usar o conceito do divisor de tensão:
Meu amigo! Depois dessa eu só digo uma coisa, eu não digo é nada! E digo mais: Só digo isso!
Resposta
a)
b)
c)
d)
e)
f)