Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.4 - Ex. 4
Se a tensão nodal no nó da Fig. 9.3 é , mostre que as duas equações nodais são
E
Diferencia a segunda destas equações e substitua no resultado valor de da primeira equação para obter uma equação originada da Fig. 9.3
Passo 1
Beleza, primeiro passo aqui vai ser encontrar as nossas equações nodais olhando para o circuito dado e então, vamos fazer o que é pedido no enunciado para obter a equação final.
O circuito dado é:
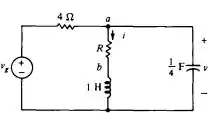
Avaliando o nó , temos que as correntes que chegam e saem desse nó são:
E sabendo que no nó , a tensão é igual a e que no nó a tensão é igual a , teremos:
Também podemos avaliar o nó , onde teremos as correntes:
Pelo desenho, temos que a corrente do indutor é a corrente indicada, portanto:
Passo 2
Pronto, mostramos que temos as duas equações nodais a partir da análise do nó e do nó do nosso circuito, agora, vamos fazer conforme pedido no enunciado, diferenciar a segunda equação e então substituir na primeira.
Diferenciando a segunda equação:
Agora vamos obter o valor de a partir da primeira equação, o que temos é:
Multiplicando por para retirar as frações:
Podemos também diferenciar essa equação, afim de obter
Como é a tensão da fonte, que é contínua, sua derivada é zero.
Passo 3
Substituindo e na segunda equação, teremos:
E por fim, agrupando termos, teremos:
E pra deixar bonito, podemos multiplicar por para deixar a segunda derivada sozinha.