Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 66
Nos terminais a-b, obtenha os circuitos equivalentes de Thévenin e de Norton para o circuito representado na Figura 10.109. Suponha .
Passo 1
Vamos lá galera! Primeiro, temos que transformar os componentes que estão no domínio do tempo e transformar para o domínio da frequência. Fazemos isso para possibilitar os cálculos!
Passo 2
Agora, vamos atrás da impedância de Thevenin! Com base no circuito abaixo, temos:
Pela divisão de tensão, podemos achar em função de :
E pelas equações nodais:
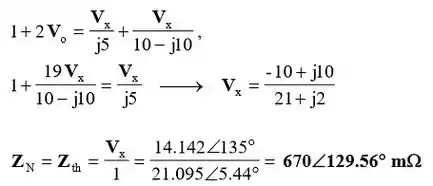
Passo 3
Para acharmos a tensão de Thevenin e a corrente de Norton é um pouco mais complicado, mas vamos com calma que vai dar certo! Primeiro, vamos considerar o circuito abaixo:
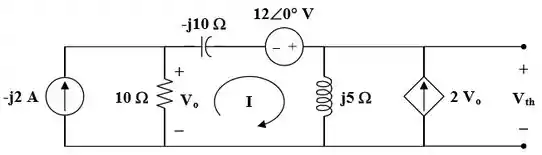
Onde,
Portanto,
Passo 4
Isolando ,
Agora é só ir pro abraço!
Resposta
Exercícios de Livros Relacionados
11.36) Calcule a corrente i em regime permanente, usando o princípio da proporcionalidade.
11.32) Substitua o circuito à esquerda dos terminais a-b por seu equivalente de Norton e calcule V.
Use transformações de fonte para determinar o circuito equivalente de Thévenin em relação aos terminais a,b para o circuito da Figura P9.45.
Determine o circuito equivalente de Norton em relação aos terminais a,b para o circuito da Figura P9.50 quando Vs = 5l0 V..
O circuito da Figura P9.51 está funcionando a uma frequência de 10 rad/s. Suponha que a seja real e esteja entre -10 e + 10, isto é, - 10≤∝≤ 10 . a) Determine o valor de a de modo que a impedância de