Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 8

8. Usando análise nodal, determine no circuito da figura

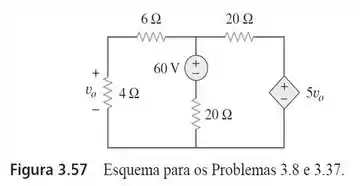
Passo 1

Bom! A primeira coisa que devemos saber antes de resolver essa questão é que a corrente elétrica irá sempre se deslocar de um ponto de maior potencial pra um de menor potencial.

E a segunda coisa que temos que fazer é de dar nomes aos bois. Essa figura tá meio vazia, né não? Precisa de um toque de classe, não concorda!?

Por isso, o que devemos fazer é dar uma embelezada nesse circuito de forma que ele possa estar mais compreensível para realizarmos a nossa análise nodal. Vamos lá...

Aqui está nossa obra de arte:

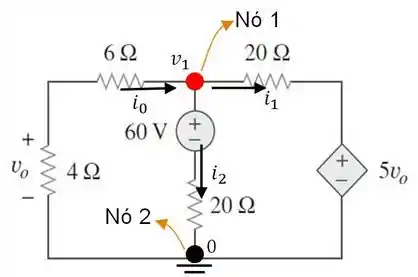
Passo 2

Nosso circuito possui nós, sendo que o nó de número está ligado à terra e portanto, possui potencial nulo.

Com isso, aplicando a para o nó , temos que:

Uma vez que a corrente sai sempre do maior para o menor potencial, vamos determinar agora as equações das correntes em relação às tensões em cada resistor:

E substituindo em seguida essas fórmulas, na relação que obtivemos do , chegamos à seguinte equação:

Passo 3

Agora, bora botar a caixola pra raciocinar um pouco. Como podemos ver na figura abaixo, mais uma vez...

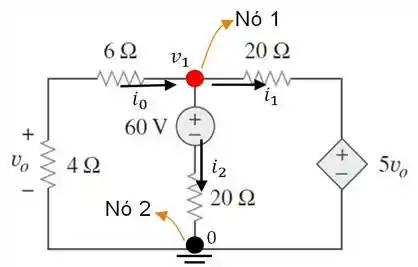
é o produto da corrente pela resistência de . Já é o produto da corrente pela resistência da associação em série entre e . E o que tudo isso quer dizer?