Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.6 - Ex. 1c

Usando fasores, calcule a corrente em regime permanente i se v = 12 cos ⁡ ( 1000 t + 30 ° )   V em (a) Fig. 10.9(a) para R = 4   k Ω , (b) Fig. 10.11(a) para L = 15   m H e (c) Fig. 10.13(a) para C = 1 2   μ F .

Passo 1

Faaaala meu povo!! Como vocês estão? Bora lá resolver mais uma questãozinha?

O primeiro passo consiste em observar o diagrama e identificar as informações dadas:

v = 12 cos ⁡ 1000 t + 30 ° V

C = 1 2 μ F

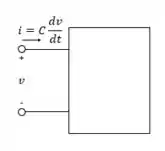
Passo 2

De v , temos:

w = 1000   r a d / s

θ = 30 °

V m = 12 ∠ 30 °   V

Desenvolvendo i = C d v d t

i pode ser dado por:

i = I m e j ( w t + ϕ )

v pode ser dado por:

v = V m   e j ( w t + θ )

Passo 3

Substituindo, teremos:

I m e j ( w t + ϕ ) = C d d t V m   e j w t + θ = j w C   V m   e j ( w t + θ )

Se dividirmos pelo fator e j w t , teremos:

I m = j w C   V m

Portanto:

I m = j w C   V m → I m = j × 1000 × 1 2 × 10 - 6 × 12 = j 6 × 10 - 3   A

Sabemos que j = 1 ∠ 90 ° , portanto teremos:

I = 6 ∠ 90   m A

Nesse caso, no domínio do tempo temos:

i = I m cos ⁡ w t + ϕ ,   onde ϕ = θ - 90 °

Passo 4

Desse modo:

i = 6 cos ⁡ ( 1000 t + 30 ° + 90 ° )

i = 6 cos ⁡ 1000 t + 12 0 ° A

Então é isso pessoal! Bons estudos e bora pra próxima...

Resposta

i = 6 cos ⁡ 1000 t + 120 ° A

Exercícios de Livros Relacionados

Calcule os valores exatos para as respostas dadas no Ex. 15.5.1.
Resolva o Exercício 10.2.2 por meio do circuito fasorial.Por meio de circuito fasorial
Calcule a tensão em regime permanente v no Exercício 10.4.1(b) usando circuito fasorial.
Uma tensão V m sin ⁡ w tV , um resistor R e um indutorL estiio em serie. Mostre que a resposta forçada i e idêntica a 10.12 , exceto que 0 cosseno substituído pelo seno dos dois modos a seguir indicad
Calcule w L no e x e r c í c i o11.4 . 1 , í tal que I mI tenha seu maior valor negativo. Tambem calculeI para este caso.