Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 25

Usando a Figura 8.78, elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos R L C sem fontes.

Passo 1

Relaxa, galera. Vamo se Ligar e achar a Resposta. Questão bem tranquila pessoal! Os papeis se inverteram! Vamos elaborar um problema nesse modelo:

Na figura abaixo, calcule i 0 t e   v o t   para t > 0 .

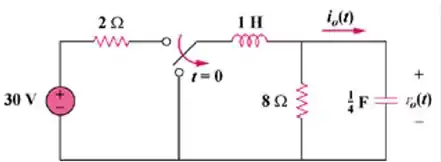
Passo 2

Em t = 0 -

v o 0 = 8 2 + 8 30 = 24

Para t > 0 , temos um circuito pararelo R L C sem fontes!

α = 1 2 R C = 1 4

ω o = 1 L C = 1 1 × 1 4 = 2

Como α é menor que o ω , temos um sistema subamortecido!

Passo 3

Por ser subamortecido, ele segue esse comportamento:

Em t = 0 , temos d v o 0 d t = 0 = - α A 1 + ω d A 2 . Mas A 2 = α ω d A 1 =

= 1 4 × 24 1.9843 = 3.024

Portanto

v o t = ( 24 cos ⁡ 1.9843 t + 3.024   s e n   1.9843 t ) e - t 4   V

E

i o t = - 12.095 s e n 1.9843 t e - t 4   A

Resposta

v o t = ( 24 cos ⁡ 1.9843 t + 3.024   s e n   1.9843 t ) e - t 4   V

E

i o t = - 12.095 s e n 1.9843 t e - t 4   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema mecânico tem como modelo um circuito R L C em série. Deseja-se uma resposta com amortecimento supercrítico com constantes de tempo 0,1m s e 0,5m s . Se for usado um resistor de 50k Ω , dete
Para o circuito da Figura 8.58, a tensão no capacitor em t = 0 - (logo antes da chave ser fechada) é:(a) 0 V (b) 4 V(c) 8 V (d) 12 V
Obtenha v ( t ) para t0 no circuito da Figura 8.73.
Obtenha v ( t ) para t0 no circuito da Figura 8.73.
Para o circuito da Figura 8.58, a corrente inicial no indutor (em t = 0) é:(a) 0 A (b) 2 A (c) 6 A (d) 12 A