Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 18
Obtenha para no circuito da Figura 8.73.
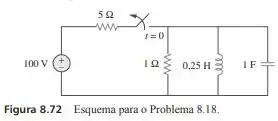
Passo 1
Faala ae! Beleza? Bora resolver esse exercício.
Primeiro, vamos analisar o circuito em , ou seja, em um tempo beeemmmm pertinho de , mas antes dele.
Só que, como podemos supor condições de estado estável, isso quer dizer que podemos considerar que o circuito ficou desse jeito por muito tempo e, então o capacitor funciona como um circuito aberto e o indutor como um curto:
E, daqui, vamos tirar a informação de que deve ser igual a , pois a tensão no capacitor não pode variar instantaneamente. Repare que aquela resistência de foi curto-circuitada, beleza? Dessa forma, a tensão no capacitor , pois é uma tensão num curto.
Já a corrente do indutor vai ser a corrente no curto. Para achar ela, podemos só calcular a corrente no circuito todo:
Beleza? Essas são nossas condições iniciais.
Passo 2
Agora, vamos analisar o circuito para .
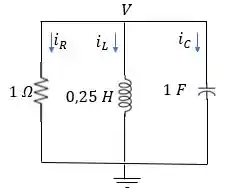
E vamos usar essa análise nodal:
Substituindo as correntes em função das tensões:
Derivando isso em relação a :
Agora, vamos arrumar e resolver essa EDO:
A equação característica é:
Substituindo os valores de e :
Resolvendo por Bhaskara:
Assim, temos as raízes:
O que nos leva a seguinte solução da EDO:
Passo 3
Usando as condições iniciais, sabemos que a tensão no capacitor deve ser em . Como é a tensão no capacitor:
E:
Assim:
Já a outra condição é de que . Da equação nodal, temos:
E sabemos que , então . Vamos isolar então:
Lembra que o resistor de era curto-circuitado em ? Então, , substituindo:
Agora, vamos derivar nosso e usar essa relação que achamos:
Então:
Fazendo as contas:
Ufa! Nossa resposta completa será: