Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 26
a) Usando os valores dos componentes do apêndice H, combine, pelo menos, um resistor e um indutor em paralelo para criar uma impedância de 40 + j20 a uma frequência de 5.000 rad/s. (Sugestão: use os resultados do Problema 9.19.)
b) Usando os valores dos componentes do apêndice H, combine, pelo menos, um resistor e um capacitor em paralelo para criar uma impedância de 40 - j20 a uma frequência de 5.000 rad/s. (Sugestão: use o resultado do Problema 9.21.)
Passo 1
Faaaaala, pessoal!! Bora resolver mais uma questão juntos?
Para esse exercício, vamos usar a notação e os resultados do problema 9.19:
Então:
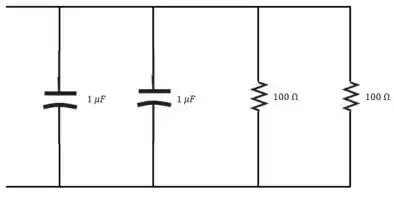
O circuito, usando os componentes do apêndice H, está mostrado abaixo:
Passo 2
Em seguida, para determinarmos o item (b), usando a notação e os resultados do problema 9.21, temos:
Então:
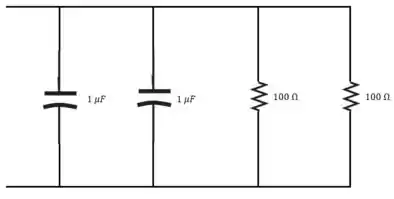
O circuito, usando os componentes do apêndice H, estão mostrados abaixo:
Prontinho, pessoal!! Bem tranquilo, não é mesmo? Bora resolver mais uma questão juntos?
Resposta
a)
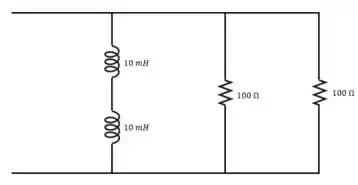
b)
