Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 85
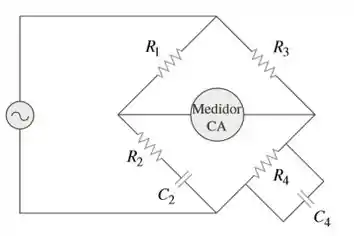
O circuito CA em ponte da Figura 9.85 e chamada ponte de Wien. Ele é usado para medir a frequência de uma fonte. Demonstre que quando a ponte está equilibrada,
Passo 1
Ponte de Wien, saber esse tipo de questão é bem importante para o aprendizado geral de circuitos C.A, porque envolve muita coisa legal! Mas calma, por envolver muita coisa n quer dizer que vá ser difícil, vamos lá!
Temos que,
Mas,
Passo 2
Agora vamos desenvolver isso com os valores que já temos!
Igualando as componentes reais e imaginarias, temos que:
Passo 3
Dividndo essas equações,
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule H ( s ) se a resposta é (a) I 1 ( s ) , (b) I 0 ( s ) e (c) V 0 ( s ) .
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °
Calcule a impedância vista pelos terminais da fonte na Figura 10.4, nas formas retangular e polar.
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °