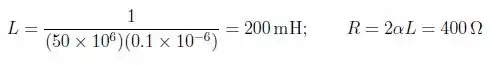Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 58
A tensão em um capacitor de 100 nF, no circuito da Figura 8.15, é descrita da seguinte forma:
depois que a chave esteve fechada durante vários segundos, a tensão é constante em 100 V. Na primeira vez que a tensão passa de 100 V, ela alcança um pico de 163,84 V. Isso ocorre p/7 ms depois do fechamento da chave. Na segunda vez que a tensão passa de 100 V, ela alcança um pico de 126,02 V. Esse segundo pico ocorre 3p/7 depois do fechamento da chave. No instante em que a chave é fechada, não há nenhuma energia armazenada no capacitor, nem no indutor. Determine os valores de R e L. (Sugestão: resolva primeiro o Problema 8.57.)
Passo 1
Fala meu povo, tudo belezinha? Temos a expressão da questão passada, que:
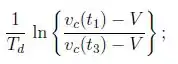
Logo,
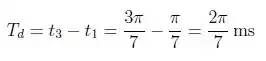
Sabendo disso:
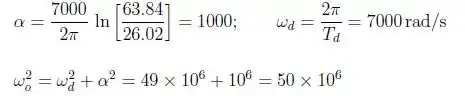
Passo 2
Por fim,
Resposta
Exercícios de Livros Relacionados
Para t0 no EX. 9.7 . 2 , calcule:a) v b) i
Calcule i , v , (d i)/(d t) e (d v)/(d t) e m t = 0^+ (d x)/(d t) + 2 x + int_0^t x d t = f ( t ) x (0) = - 1
Calcule a equação diferencial satisfeita por i no circuito,Use este resultado para calcular i para t0 , se R = 10 Ω ,L = 2 H ,C = 0,05 F ,v 0 = 0 e i 0 = 6 A .
Quanto maior o valor de R, menor o amortecimento que existirá no cabo de um circuito subamortecido paralelo RLC (porque α = 1 2 R C ) . Assuma R = ∞ (circuito aberto) e mostre que, no caso sem fontes,