Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 47
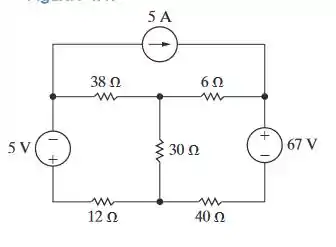
a) Use o método das correntes de malha para determinar a potência que a fonte de corrente de 5 A fornece ao circuito da Figura P4.47.
b) Determine a potência total fornecida ao circuito.
c) Verifique seus cálculos mostrando que a potência total gerada no circuito é igual à potência total dissipada.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - Vamos definir as malhas primeiramente, a esquerda inferior será , a da direita inferior igual a e a superior nós já temos um valor definido (que é igual a ). Aplicando o método das correntes de malha na inferior esquerda, nós temos que
Simplificando um pouco as coisas...
Já na malha inferior à direita, nós obtemos o seguinte resultado
Simplificando, nós temos que
Nós temos o seguinte sistema
Que tem como resultado
Passo 2
Agora, vamos calcular a tensão aplicada na fonte de corrente de 5 A usando o método das correntes de malha
Simplificando um pouco mais as coisas
Partindo para a potência desenvolvida nessa fonte, temos
Substituindo os valores, nós obtemos que
Uma vez que a potência é negativa, portanto, esta fonte de corrente fornece potência, assim,
Passo 3
B – Calculando a potência desenvolvida pela fonte de tensão de 67 V, com isso, nós temos que
Logo
Como o valor é positivo, logo, esta fonte absorve potência. Partindo para a fonte de tensão de 5 V, temos
Substituindo os valores,
Como o valor da potência é positiva, portanto, esta fonte de tensão absorve
Passo 4
C – Calculando a potência dissipada pelos resistores, nós temos que
Que vai ser igual a
Calculando a potência total dissipada
Substituindo os valores, nós obtemos que
Logo, a potência dissipada é igual a potência total desenvolvida, portanto,