Repita o Ex. 3.2.1 se o resistor de 2Ჲ for trocado por um resistor de 4Ჲ. (Note que uma resistência negativa e possível, quando uma fonte dependente está presente.)
Passo 1
Resolvemos esse exercício utilizando o método de análise de malhas da seguinte maneira.
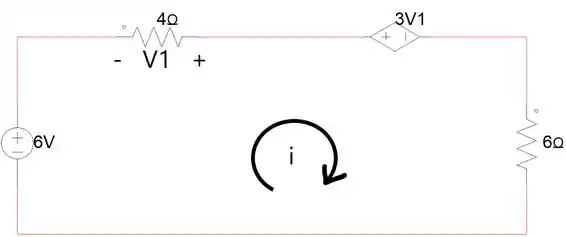
Temos apenas uma malha, portanto teremos uma equação.
Passo 2
Obtemos a equação: .
Também podemos obter a equação de :
Passo 3
Substituindo a equação na primeira equação, podemos isolar o .
Sabendo , podemos agora obter pela equação:
Passo 4
Por fim, para encontrar a resistência vista pela fonte é .
Ჲ
Resposta
Ჲ