Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 1.Problemas - Ex. 7
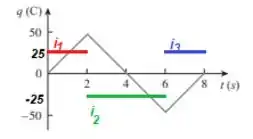
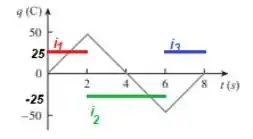
1.7 A carga que flui por um fio é representada na Figura 1.24. Represente a corrente correspondente.
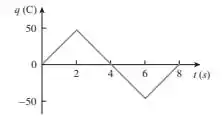
Passo 1
A primeira coisa que devemos fazer aqui é encontrar a equação das retas representam a variação de carga. Vamos as renomear de...
Lembre-se toda reta pode ser então representada pela equação:
Passo 2
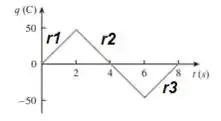
Vamos começar com a primeira retinha (r1).
Para encontrar a equação de uma reta, precisamos de dois pontos sempre. Nesse caso, o primeiro ponto é a origem , e o segundo ponto, podemos tomar como sendo o ponto .
Agora, jogar os dois pontos na equação geral da reta:
Da primeira equação na segunda...
Então a reta 1 é...
Passo 3
Vamos agora encontrar a equação da reta r2 de modo análogo:
Então primeiro temos que procurar por dois pontos pertencentes a essa reta: o primeiro pode ser o e o segundo, pode ser o ponto (bem no meio da reta cortando o eixo). Agora simbora substitui-los na equação geral:
Da segunda equação, tiramos que...
Jogando na primeira...
Portanto... . E a equação da reta r2 então é...
Passo 4
Por último, vamos buscar a equação da reta r3 que possuem como pontos auxiliares para a determinação de sua equação, os pontos: e de modo que...
Da segunda equação...
Jogando na primeira...
E, portanto...
A reta r3 então será...
Passo 5
Com a equação de todas as retas então em mãos:
E sabendo que a corrente nada mais é do que a derivada temporal da carga ()...
Claro, como a derivada está apenas definida no intervalo (aberto) de definição da função de cada reta...
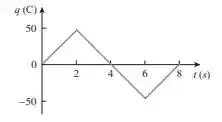
E observando que o intervalo de r1 é de a , o de r2, é de a , e por último o intervalo de r3 é de a , teremos...
Podemos agora desenhar essas retas sob o mesmo gráfico (retas constantes e que passam pelo respectivo valor no eixo ):
Resposta
