Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 59
a) Use os valores dos componentes do Apêndice H para criar um circuito RC de primeira ordem (veja a Figura 7.21) com uma constante de tempo de 250 ms. Use um único capacitor e uma rede de resistores, se necessário. Desenhe seu circuito. b) Suponha que o capacitor que você escolheu em (a) tem uma queda de tensão inicial de 100 V. Em t = 0, uma chave conecta uma fonte de corrente com valor de 1 mA em paralelo com o capacitor e o resistor equivalente. Escreva uma expressão para a queda de tensão no capacitor para t $ 0. c) Usando o resultado obtido em (b), calcule o tempo em que a queda de tensão no capacitor atinge 50 V.
Passo 1
[a] – Como se pode notar, existem várias soluções para o problema, tirando como base a seguinte fórmula:
Escolhendo um capacitor de do apêndice H, temos
Já deu para perceber que vamos ter que utilizar alguma combinação de resistores para fazer uma manipulação, nesse caso de resistores em série.
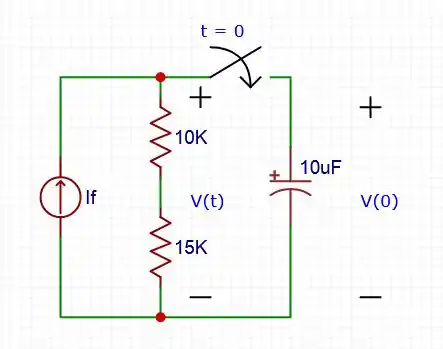
Passo 2
[b] – Utilizando a equação geral da tensão:
E
Passo 3
[c] –
Logo,