Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 55

A chave do circuito visto na Figura P7.55 esteve na posição a por um longo tempo. Em t = 0, a chave passa instantaneamente para a posição b. Determine vo (t) e i o (t) para t $ 0+.

Passo 1

Para t < 0 :

i 0 0 - = 20 100 10 × 10 - 3 = 2   m A

v 0 0 - = 2 × 10 - 3 50000 = 100   V

Quando t = ∞ o capacitor se comporta como um circuito aberto, logo:

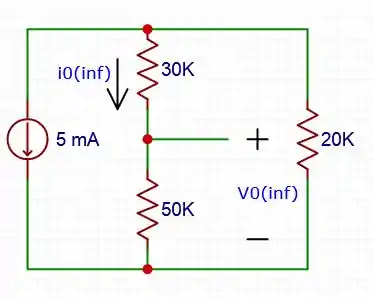
Para encontrar i 0 ( ∞ ) , é fazer a combinação entre os resistores:

i 0 ∞ =   - 5 × 10 - 3 20 100 = - 1   m A

E para v 0 ( ∞ ) , temos a seguinte relação: v 0 ∞ = i 0 ( ∞ ) ( 50 k Ω )

v 0 ∞ = i 0 ∞ 50000 =   - 50   V

Passo 2

Para t ≥ 0 : Fazendo algumas modificações no circuito, temos:

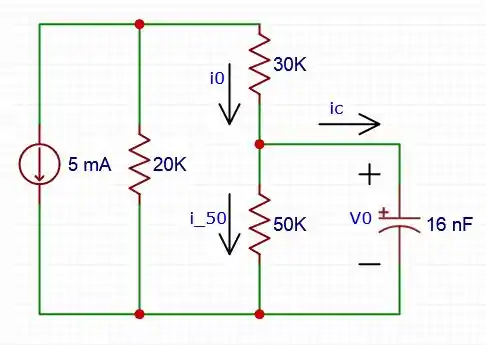
A resistência equivalente é igual a:

R t h = 50000 2 50000 + 50000 = 25   k Ω

E como o capacitor é 16   n F , a constante de tempo é igual a:

τ = 25000 16 × 10 - 9 = 0,4   m s

E a sua inversa:

1 τ = 2500

Com isso, podemos encontrar a equação de tensão:

v 0 t =   - 50 + 150 e - 2500 t   V .       t ≥ 0

A corrente no capacitor segue a seguinte relação i c = C d v 0 d t , logo:

i c = C d v 0 d t =   - 6 e - 2500 t   m A ,     t ≥ 0 +

E no resistor de 50 k Ω :

i 50 k = v 0 50000 =   - 1 + 3 e - 2500 t   m A ,     t ≥ 0 +

E finalmente, a corrente i 0 é a soma das duas correntes:

i 0 = i c + i 50 k =   - ( 1 + 3 e - 2500 t )   m A ,     t ≥ 0 +

Resposta

a )   v 0 t =   - 50 + 150 e - 2500 t   V .       t ≥ 0

b )   i 0 =   - ( 1 + 3 e - 2500 t )   m A ,     t ≥ 0 +  

Exercícios de Livros Relacionados

Calcule v para t0, se o circuito está em regime permanente em t = 0 - .
Calcule v para t0 se o circuito está em regime permanente em t = 0 - .
8.10) Calcule v para t0, se o circuito está em regime permanente em t = 0-.
Um circuito está em regime permanente em t0 e a chave é mudada da posição 1 para a posição 2 em t = 0 . Calcule v para t0 .
Calcule i para t0 , se o circuito está em regime permanente em t0 .