Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 40
a) Use os valores dos componentes do Apêndice H para criar um circuito RL de primeira ordem (veja a Figura 7.16) com uma constante de tempo de 8 ms. Use um único indutor e uma rede de resistores, se necessário. Desenhe seu circuito. b) Suponha que o indutor que você escolheu em (a) não tenha nenhuma energia inicial armazenada. Em t = 0, uma chave conecta uma fonte de tensão com um valor de 25 V em série com o indutor e o resistor equivalente. Escreva uma expressão para a corrente no indutor para t $ 0. c) Usando o resultado obtido em (b), calcule o tempo em que a corrente no indutor atinge 75% de seu valor final.
Passo 1
[a] - Note que há muitas diferentes soluções para esse problema, ele pede valores que são disponibilizados no apêndice H, então vamos resolver.
Primeiro, vamos começar com a constante de tempo.
Escolhendo um indutor de (do apêndice H, obviamente hehe), então:
Combinando resistores de , todos em série:
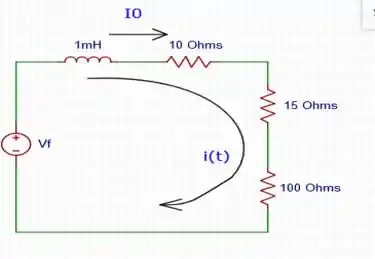
Passo 2
[b] – Usando a equação geral das correntes, temos:
Como e usando a lei de Ohm para calcular o
Então, podemos calcular o , dessa forma aqui:
Passo 3
[c] – Fazendo a igualdade entre os termos, podemos encontrar a porcentagem pedida
Fazendo a inversão:
Jogando o logaritmo neperiano, temos: