Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 65
Se o pulso de entrada na Figura 7.130a for aplicado ao circuito da Figura 7.130b, determine a resposta i(t).
Passo 1
Primeiro vamos analisar o sinal proposto. Note que ele é a soma de dois outros sinais, a imagem abaixo ilustra:
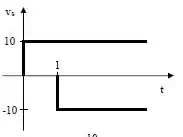
Assim, podemos dizer que o sinal é:
Sabendo disso, vamos analisar agora o circuito proposto, note que para o cálculo da constante de tempo devemos curto-circuitar na fonte de tensão, assim temos dois resistores em paralelo. Com isso,
Passo 2
Certo! Agora que já obtemos a constante de tempo e a função que representa o sinal. Já podemos obter as equações da corrente, para isso vamos separar para 3 instantes de tempo.
Para t
Note que, a tensão para t
Para 0
Para este intervalo de tempo a tensão é igual a 10 V, e como o indutor pode ser substituído por um curto circuito não temos interferência da resistência de 20. Assim,
Substituindo em,
Obtemos,
Podemos tirar dessa equação que
Para t>1,
Note que, como não há sinal para t>1 então,
Substituindo em,
Resposta
Resposta
Ei, a resposta está no passo a passo :)