Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 63

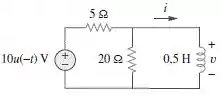
Obtenha v(t) e i(t) no circuito da Figura 7.128.

Passo 1

Primeiro vamos calcular a constante de tempo. Observe que, se dermos curto na fonte teremos dois resistores em paralelo, ou seja,

R_e q = 5 | | 20 = 4 omega

Portanto, sabemos que

tau = (L)/(R) = (0.5)/(4) = (1)/(8)

Passo 2

Agora vamos analisar o circuito. Observe as fontes de tensão, teremos 2 instantes.

Para t

u (- t) = 1

E como podemos substituir o indutor por um curto, assim a corrente não passa pelo resistor de 20 omega , então,

i (0) = (v)/(R) = (10)/(5) = 2 A

Para t>0:

u (- t) = 0

Consequentemente,

i (oo) = 0

E como,

i (t) = i (oo) + [i (0) - i (oo)] e^(- t // tau)

Temos:

i (t) = 2 e^(- 8 t) u ( t ) A

Passo 3

Como já obtemos a corrente que passa pelo indutor, para obtermos a tensão basta utilizar a equação:

v (t) = L (d i)/(d t)

Desse modo,

(d i)/(d t) = (- 8) * (2) e^(- 8 t) u (t)

Portanto,

v (t) = (1)/(2) * ( - 16 ) e^(- 8 t) u (t)

v (t) = - 8 e^(- 8 t) u (t) V

Resposta

i (t) = 2 e^(- 8 t) u ( t ) A

v (t) = - 8 e^(- 8 t) u (t) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule i para t0 se o circuito está em regime permanente cc em t = 0 - .
Calcule i para t0 no circuito do Ex. 8.6.2, se as duas chaves são fechadas em t = 0 e i 0 = 0 . (Sugestão: Calcule i como antes e observe que i f é devida às duas fontes.)
Calcule v e i para t0 , se seu circuito está em regime permanente cc em t = 0 - .
CaIcule a resposta i para v R = 42u t V .
8.30) Calcule v1 para t0, se não existe energia inicial armazenada.