Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 48

O valor de pico da tensão da fonte senoidal do circuito da Figura P10.48 é 180 V, e sua frequência é 5.000 rad/s. O resistor de carga pode variar de 0 a 4.000 V e o capacitor de carga pode variar de 0,1 mF a 0,5 mF.

a) Calcule a potência média fornecida à carga quando Ro = 2.000 V e Co = 0,2 mF.

b) Determine os valores de Ro e Co que resultarão na maior potência média transferida a Ro. c) Qual é a maior potência média em (b)? Ela é maior do que a potência em (a)?

d) Se não houver restrições a Ro e Co, qual será a máxima potência média que pode ser fornecida a uma carga?

e) Quais são os valores de Ro e Co para a condição em (d)? f) A potência média calculada em (d) é maior do que a calculada em (c)?

Passo 1

Beleza pessoal?! Como estão?! Espero que estejam super ligados para darmos continuidade a uma excelente resolução com o padrão Responde Aí de qualidade. Então peguem seus lápis e papel e vem comigo.

  1. Vamos determinar a impedância do indutor de 0.6   H ,

    2. Z 6 m H = j ω L

    = j 5000 0.6

    = j 300 Ω

    Agora iremos determinar a impedância da carga do capacitor de 0.2   μ F

    Z 0.2 μ F = 1 j ω C

    =   1 j 5000 0.2 ∙ 10 - 6

    = - j 1000   Ω

    Passo 2

    Agora meu caro aluno, desative a fonte de tensão e desconecte a impedância da carga e determine a impedância equivalente de Thevenin Z T h

    Z T h   =   ( 6000 | | 12000 )   + j 3000

    =   6000 12000 6000   +   12000   +   j 3000

    = 4000 + j 3000 Ω

    Desconecte a impedância da carga e determine a tensão equivalente de Thevenin V T h

    V T h = 12000 6000   +   12000 180

    = 120   V

    Conectaremos agora a impedância de carga ao circuito equivalente de Thevenin conforme mostrado na Figura. Assim iremos determinar a corrente que flui através da carga I

    I   =   V T h Z T h + Z 0

    =   120 6000   +   j 2000

    =   18   -   j 6   m A

    Agora determine a potência média dissipada na resistência de carga P

    P = 0.5 I 2 R 0

    = 0.5 18 2 + 6 2 2000

    =   360   m W

  2. Considerações a serem feitas; a potência média entregue à carga é máxima quando Z 0 , mas isso não pode ser alcançado devido às restrições em C 0 e R 0

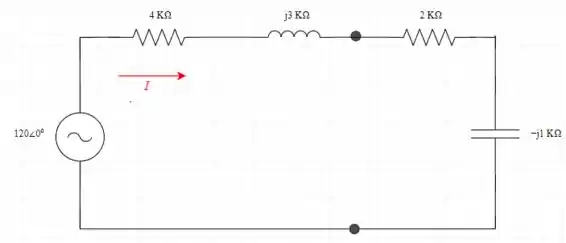
    3. A condição ideal para X 0 é

    X 0 = - X T h

    para obter o X 0 mais próximo de - X T h , use uma capacitância de 0 . 1   μ F

    X 0 = - 1 ω C

    =   - 1 ( 5000 ) ( 0.1 ∙ 10 - 6

    = - 2000   Ω

    O valor ótimo da resistência de carga R 0 é dado por

    R 0 = R T h 2 + X L + X T h 2

    =   4000 2 + 3000 + 2000 2

    = 4123.1   Ω

    O valor do resistor mais próximo é dado por

    R 0 = 4000   Ω

    C 0 = 0.1 μ F

    Passo 3

  3. Determine a corrente que flui através da impedância de carga I

    4. I   =   V T h Z T h + Z 0

    =   120 8000   +   j 1000

      =   14.77   -   j 1.85   m A

    Agora determine a potência média dissipada na resistência de carga P

    P = 0.5 I 2 R 0

    = 0.5 1 4.77 2 + 1.85 2 4 000

    =   443.1   m W

    A potência média é maior do que em (a), uma vez que as condições ótimas para o resistor de carga e o capacitor são usadas confortavelmente em (c)

    S i m ,   P   =   443.1   m W   >   P   =   360   m W

    Passo 4

  4. Se você resistiu até aqui na resolução, lhe digo que tem mais. Para entregar a potência média máxima à carga, a impedância de carga Z0} é dada por

    5. Z 0 = Z T h *

    = 4000 - j 3000 Ω

    Agora iremos determinar a corrente que flui através da impedância de carga I,

    I   =   V T h R T h + R 0

      =   120 8000

    =   15   m A

    Agora determine a potência média dissipada na resistência de carga P

    P = 0.5 I 2 R 0

    = 0.5 0.015 2 4000

    =   4 50   m W

  5. A resistência de carga R 0 é dada por,

    6. R 0 = R T h

    = 4000   Ω

    A indutância de carga X 0 é dada por,

    X 0 = - X T h

    = - 3000 Ω

    Portanto, a capacitância de carga C 0 é dada por

    C 0 = 1 ω X C

    =   1 5000 3000

    =   66.67   n F

  6. FINALMENTE A ÚLTIMA

A potência média em (f) é máxima desde que a impedância de carga corresponda à impedância equivalente de Thevenin

Z 0 = Z T h *

Resposta

Veja a resolução amigo, please.

Exercícios de Livros Relacionados

Um aquecedor industrial tem uma plaqueta do fabricante indicando o seguinte: 210 V/60 Hz/ 12kVA/ FP de 0,78 (atrasado). Determine as potências aparente e complexa e a impedância do aquecedor.
Um amplificador de potência tem impedância de saída igual a 40 – j8 Ω . Ele produz uma tensão de saída sem carga de 146 V a 300 Hz. Determine a impedância da carga para obter a máxima transferência de
Um sistema de transmissão de potência tem como modelo aquele mostrado na figura abaixo. Se V s=240 ∠ 0 ° RMS, determine a potência média absorvida pela carga.
Um capacitor de acoplamento é usado para bloquear corrente CC de um amplificador, como mostra a figura. O amplificador e o capacitor atuam como uma fonte, enquanto o alto-falante é a carga como indica
Conforme mostrado na Figura 11.97, uma linha de alimentação de 550 V alimenta uma planta industrial formada por um motor que consome 60 kW com FP 0,75 (indutiva), um capacitor com potência nominal 20