Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 10
a) Verifique se a Equação 9.9 é a solução da Equação 9.8. Isso pode ser feito substituindo-se a Equação 9.9 no lado esquerdo da Equação 9.8 e, então, observando se o resultado é igual ao do lado direito para todos os valores de t . 0. Em t = 0, a Equação 9.9 deve reduzir-se ao valor inicial da corrente. b) Visto que a componente transitória desaparece com o passar do tempo e que nossa solução deve satisfazer a equação diferencial para todos os valores de t, a componente de regime permanente, por si, também deve satisfazer a equação diferencial. Verifique essa observação mostrando que a componente de regime permanente da Equação 9.9 satisfaz a Equação 9.8.
Passo 1
Saaaalve galerinha. Tudo bem com vocês? Então bora lá. Pro item a), temos que os valores numéricos dos termos da eq da 9.8 são:
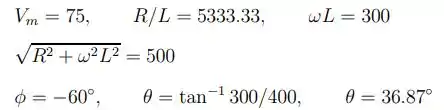
Substituindo esses valores na equação da 9.9:
Passo 2
Aqui no item b), o componente transiente:
Componente do estado estacionário:
Já no item c), temos que por direta substituição na equação 9.9 no item a,
Passo 3
No item d) resolvendo por partes, tudo está na equação! Temos:
No item e), pra finalizar, temos que a tensão corrente atrasa a tensão em 36.87 graus.