Introdução aos Transformadores
Produzido por Alexandre NunesTeoria
As usinas geradoras de energia geram tensões muito elevadas, por volta de . Essa tensão gerada é elevada à níveis acima de na transmissão, depois abaixada para novamente e, por fim, é abaixada mais uma vez para para atender os consumidores.
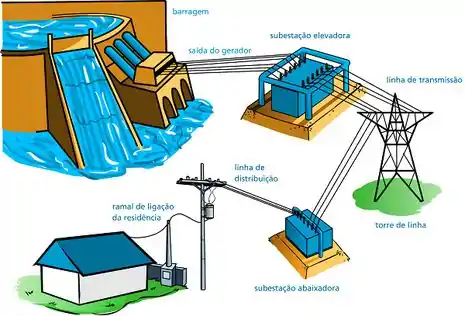
Então, desde a geração até chegar nas tomadas das nossas casas, a tensão é abaixada e elevada diversas vezes e o equipamento responsável por essa transformação nos valores de tensão é o Transformador.
Com certeza você já deve ter visto um bicho desses pendurado nos postes das ruas perto de sua casa:

Esse é um transformador trifásico de distribuição. É ele que abaixa a tensão de para .
Agora que você já tem uma ideia da importância do transformador e do que ele é capaz, vamos ver como os transformadores monofásicos elevam ou abaixam as tensões.
Transformador ideal
Tudo ou quase tudo nessa vida não é ideal, não é verdade? E com transformadores não poderia ser diferente, mas, na prática, podemos fazer aproximações muito boas e considerar o transformador como sendo ideal.
O transformador é basicamente formado por um núcleo de material ferromagnético e por dois enrolamentos de espiras, que chamamos de enrolamento do primário e do secundário do transformador. Vou fazer um desenho esquemático do transformador para você visualizar melhor:
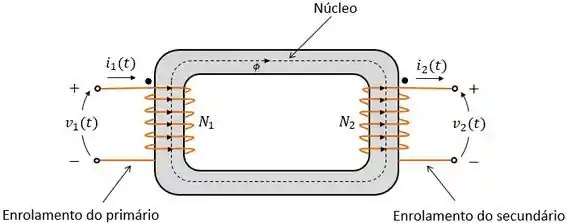
Em um transformador ideal não há perdas, ou seja, quando alimentamos o primário com uma tensão , todo o fluxo produzido pela passagem da corrente pelos enrolamentos do primário passa pelos enrolamentos do secundário.
Esse fluxo induz a tensão nos terminais do enrolamento secundário do transformador e a corrente na presença de carga conectada ao secundário.
Beleza, mas como é que a tensão no primário se relaciona com a tensão do secundário?

Então, elas se relacionam pelo número de espiras do primário e do secundário. Como estamos trabalhando com corrente alternada, faremos a análise na forma fasorial.
é chamada de relação de transformação do transformador.
Por exemplo, se alimentarmos os terminais do primário com , o número de espiras do primário for e o enrolamento do secundário tiver espiras. Qual será a tensão medida nos terminais do secundário?
Pelo enunciado, sabemos que:
Utilizando a relação de transformação, temos:
Simbolicamente podemos representar esse transformador assim:
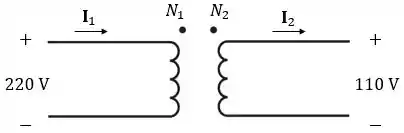
Pronto, é assim que os transformadores abaixam e elevam as tensões!
Você deve ter visto que quando eu desenho um esquema do transformador eu sempre indico duas bolinhas:
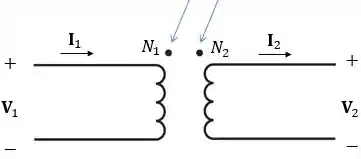
Essas bolinhas são para indicar a polaridade do transformador e o sentido com que a corrente circula pelos enrolamentos. Nós desenhamos a bolinha onde a corrente entra pelo primário e por onde ela sai no secundário.
Já a relação entre a corrente que entra no primário do transformador e a corrente que sai do secundário do transformador é
Ou
Por isso que dizemos que a relação de transformação entre as tensões do primário e do secundário são diretamente proporcionais à relação de suas espiras enquanto a de corrente é inversamente.
Das relações de corrente e tensão com o número de espiras, chegamos à conclusão de que:
Logo, a potência do primário é igual à potência instantânea de saída do secundário:
Isso era esperado, porque se trata de um transformador ideal, logo não consideramos as perdas, concorda?
Como já encontramos relação de transformação para tensão e corrente, falta agora encontrarmos uma relação de transformação para a impedância. Calma, não se desespere! A gente vai tirar de letra!
Primeiro vamos conectar uma impedância no secundário do transformador:
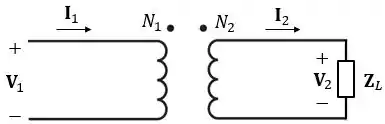
Pela lei de Ohm, sabemos que
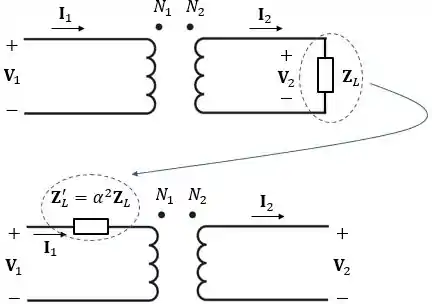
Agora, vamos ver como essa impedância é vista no primário:
Pelas relações de transformação:
Então, quando substituímos:
Logo, se queremos transformar uma impedância que está conectada no secundário para o primário, temos que usar esta relação.
Esse modo de transferir a impedância de um lado a outro do transformador é conhecido como reflexão de impedâncias.
Modelo série do transformador
Agora vamos considerar os efeitos das resistências dos enrolamentos e do fluxo disperso. Com isso, temos o modelo abaixo:
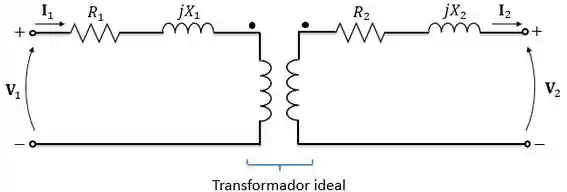
Onde:
- e representam as perdas que ocorrem por efeito Joule nos enrolamentos do primário e do secundário, respectivamente;
- e representam as perdas devido ao fluxo disperso, chamadas de reatância de dispersão, do primário e do secundário, respectivamente.
Por hora, vamos considerar apenas esses fatores no modelo do transformador. Mas, em um modelo completo também consideramos as perdas que ocorrem no núcleo do transformador e a perda mútua, que ocorre devido ao fluxo comum aos dois enrolamentos.
Para facilitar a nossa análise de circuitos com a presença de transformadores é muito comum substituímos o transformador por um circuito equivalente. Vamos ver como fazer isso passo-a-passo.
Passo 1:
Primeiro, temos que refletir ou referir todas as grandezas para o primário ou secundário do transformador. A gente faz isso utilizando aquelas relações de transformação que acabamos de estudar.
Vamos começar refletindo tudo para o primário do transformador. Sabemos que as tensões têm a seguinte relação de transformação:
Logo a tensão refletida para o primário será:
Sempre usamos apóstrofo (‘) para indicar que a grandeza está refletida.
Fazendo o mesmo para a corrente, temos:
Por último, vamos fazer o mesmo para a impedância:
Logo,
Passo 2:
Desenhamos o novo modelo com as grandezas refletidas para o primário:
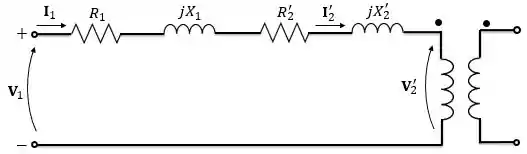
Para reduzir o modelo fazemos:
Chegando no modelo baixo:
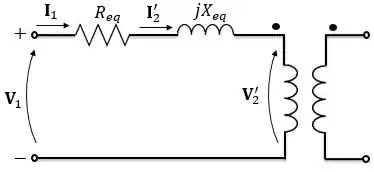
Passo 3:
Para terminar, omitimos o transformador ideal e chegamos ao circuito equivalente série referido ao primário. O circuito fica assim:
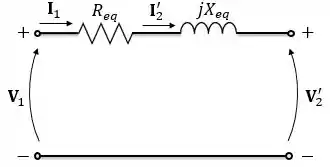
Viu só, esse é o circuito que você vai utilizar muito daqui para frente!
Se quiséssemos desenhar o circuito equivalente série referido ao secundário faríamos os mesmos passos:
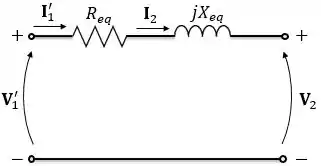
Onde,
Pronto! Agora é destruir os exercícios!
Modelo série do transformador
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.538, Problema 13.37
Um transformador elevador de tensão ideal de libera para uma carga resistiva. Calcule:
A relação de espiras.
A corrente no primário.
A corrente no secundário.
Passo 1
Vamos começar! O enunciado nos disse que o transformador é elevador. Isso quer dizer que ele recebe uma tensão menor e a transforma para uma tensão maior. Então, podemos desenhar o seguinte esquema:
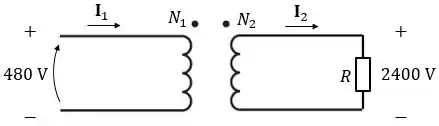
Onde a tensão do primário é
Já a do secundário:
Como não foi dito nada sobre o ângulo e a carga é resistiva não precisamos nos preocupar com defasamentos. Por isso, vamos considerar apenas os módulos dos fasores.
Passo 2
Na letra precisamos encontrar a relação de espiras do transformador, ou seja:
Sabemos que a relação entre as tensões do primário e do secundário são diretamente proporcionais à relação das espiras em um transformador.
Logo, substituindo os valores das tensões no primário e secundário, temos:
Passo 3
Na letra temos que calcular a corrente . Para isso, vamos usar a fórmula da potência:
Como , temos:
Passo 4
Pra terminar, na letra temos que calcular a corrente no secundário . Sabemos que a relação entre as tensões do primário e do secundário são diretamente proporcionais à relação de suas espiras enquanto a de corrente é inversamente.
Então,
Resposta
Exercício Resolvido #2
Lista Prof. João Salvador - UFRJ - Ex.5
O lado de alta tensão (AT) de um transformador abaixador tem espiras e o lado de baixa tensão (BT) tem espiras. Uma tensão de é aplicada ao lado de AT e uma impedância de carga de é ligada ao lado BT. Calcule:
A corrente e a tensão no enrolamento de BT.
A corrente no lado de AT.
A impedância vista dos terminais de AT (impedância do secundário refletida).
Passo 1
Vamos começar! O enunciado nos disse que o transformador é abaixador. Isso quer dizer que ele recebe uma tensão maior e a transforma para uma tensão menor. Então, podemos desenhar o seguinte esquema:
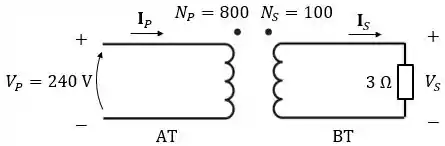
Como não foi dito nada sobre o ângulo e a carga é resistiva não precisamos nos preocupar com defasamentos. Por isso, vamos considerar apenas os módulos dos fasores.
Passo 2
Na letra precisamos encontrar a corrente e a tensão no enrolamento de BT, que está no secundário do transformador.
Sabemos que a relação entre as tensões do primário e do secundário são diretamente proporcionais à relação das espiras em um transformador.
Logo, substituindo os valores dos números de espiras do primário e do secundário, temos:
Logo, a tensão no enrolamento de baixa será:
Passo 3
Agora, vamos aplicar a lei de Ohm na carga para encontrarmos a corrente no enrolamento de BT.
Passo 4
Na letra temos que calcular a corrente no lado de AT, . Para isso, vamos usar a relação de transformação do transformador.
Passo 5
Pra terminar, na letra temos que calcular a impedância refletida para o primário. Sabemos que a relação de transformação para transferir a impedância do secundário para o primário é
Então,
Resposta
Exercício Resolvido #3
Lista Prof. João Salvador - UFRJ - Ex.5
Um transformador de , foi projetado para ter uma f.e.m. induzida de . Supondo o transformador ideal, calcule:
O número de espiras do enrolamento de alta tensão (AT), . O número de espiras do enrolamento de baixa tensão (BT), . A corrente nominal para o enrolamento de AT, . A corrente nominal para o enrolamento de BT, . A relação de transformação.
Passo 1
Com os dados que o enunciado nos fornece, vamos desenhar o esquema desse transformador:
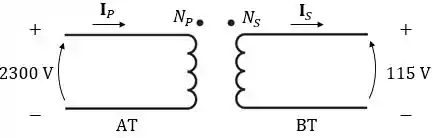
Passo 2
Na letra , precisamos encontrar o número de espiras do primário. O enunciado nos disse que a f.e.m. induzida é de , ou seja, que para cada espira temos . Logo, para encontrar o número de espiras vamos usar a equação abaixo:
Passo 3
Fazendo o mesmo para o lado de BT, temos:
Passo 4
Na letra , precisamos encontrar a corrente no primário. O enunciado nos disse que o transformador é de , ou seja,
Como,
Passo 5
Agora, vamos usar a relação de transformação do transformador para encontrarmos a corrente no lado de BT.
Logo,
Passo 6
Para terminar, na letra , temos que calcular a relação de transformação.
Resposta
Exercício Resolvido #4
Livro Sadiku, p.538, Problema 13.41
Determine e no circuito abaixo:
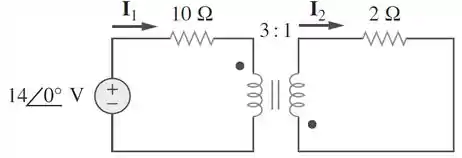
Passo 1
Primeiro, vamos determinar a corrente . Para isso, vamos ter que refletir o resistor de para o primário.
Logo, temos que usar a relação de transformação:
Mas, temos que tomar cuidado! As bolinhas que indicam a polaridade estão em posições diferentes do que a gente está acostumado. A do primário está na parte de cima do enrolamento enquanto a do secundário está na parte inferior.
Quando isso ocorre, a gente considera a relação de transformação negativa. Então,
Passo 2
Refletindo a resistência de , temos:
Portanto, o circuito equivalente série do transformador referido ao primário será:
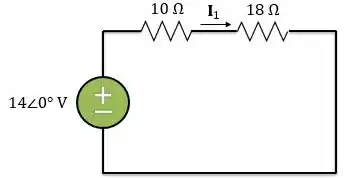
Logo, aplicando a lei de Ohm:
Passo 3
Agora, vamos calcular . Pela relação de transformação, temos:
Logo,
Esse sinal de menos indica que a corrente está no sentido contrário ao que está indicado no desenho. O que faz sentido, pois, como vimos na teria, indicamos com a bolinha onde a corrente está saindo do enrolamento do secundário.
Resposta
Exercício Resolvido #5
Livro Sadiku, p.538, Problema 13.42
Considere o circuito da figura abaixo e determine a potência absorvida pelo resistor de . Suponha que seja um valor RMS.
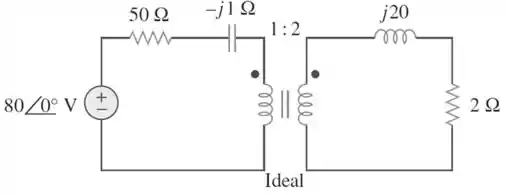
Passo 1
Precisamos determinar a potência absorvida pelo resistor de . Então, primeiro, temos que encontrar a corrente que passa por ele para aplicar a seguinte fórmula de potência:
Como o resistor de está no secundário do transformador, vamos referir todo o circuito para o secundário. Para isso, precisamos saber a relação de transformação desse transformador.
Passo 2
Agora, vamos referir as grandezas do primário para o secundário. A tensão do primário referida para o secundário será:
Já a impedância referida para o secundário será:
Então, o circuito equivalente série do transformador referido ao secundário será:
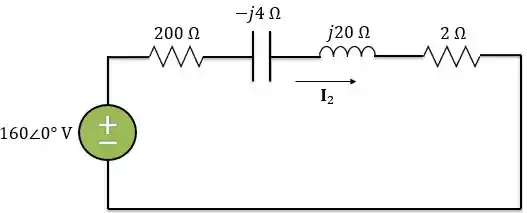
Passo 3
A impedância equivalente do circuito acima é:
Então, pela lei de Ohm, a corrente no secundário será:
Passo 4
Agora que temos a corrente que passa pelo resistor de , vamos calcular a potência que ele absorve:
Resposta
Exercício Resolvido #6
Livro Sadiku, p.539, Problema 13.50
Calcule a impedância de entrada do circuito abaixo.
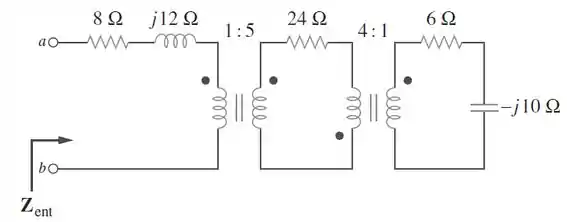
Passo 1
Nesse circuito, temos dois transformadores.
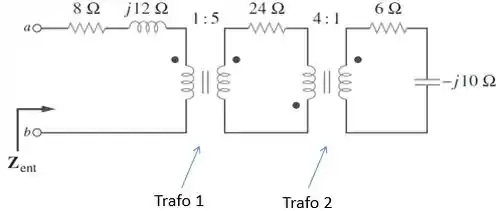
Calcular a impedância de entrada do circuito é refletir todas as impedâncias para o primário do primeiro transformador. Para isso, temos que lembrar que para refletir a impedância do secundário para o primário utilizamos a relação abaixo:
Passo 2
Primeiro, vamos refletir a impedância do secundário do transformador 2 para o seu primário. A relação de transformação desse transformador é:
A gente coloca o sinal de menos antes porque as bolinhas que indicam a polaridade estão em posições diferentes do que a gente está acostumado. A do primário está na parte de baixo do enrolamento enquanto a do secundário está na parte superior.
Quando isso ocorre, a gente considera a relação de transformação negativa.
Passo 3
Então, depois desse passo nosso circuito fica assim:
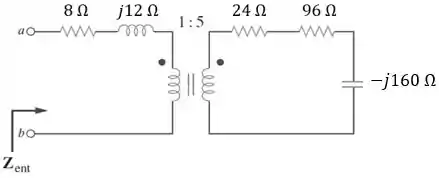
Agora, vamos refletir a impedância do secundário para o primário. Nesse transformador a relação de transformação é:
Então,
Passo 4
Pronto, todas as impedâncias estão refletidas para o primário do transformador 1. Agora é calcular a impedância de entrada.
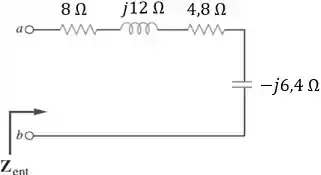
Resposta
Exercício Resolvido #7
Livro Sadiku, p.538, Problema 13.45
Considere o circuito da figura abaixo e determine a potência média absorvida pelo resistor de .
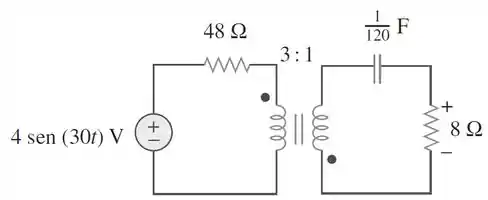
Passo 1
Primeiro temos que passar o circuito para o domínio da frequência:
Logo, no domínio da frequência, a tensão da fonte será:
Temos que passar a tensão para o valor eficaz:
Para o capacitor, temos que lembrar da fórmula:
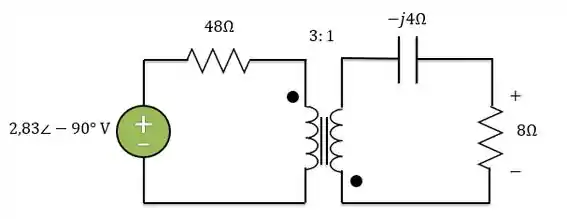
Passo 2
Pronto, agora podemos começar a resolver o circuito.
Como ele pede a potência média dissipada no resistor de , que está no secundário, vamos refletir a tensão e a impedância do primário para o secundário para calcular a corrente .
A relação de transformação será, então:
Mas, temos que tomar cuidado! As bolinhas que indicam a polaridade estão em posições diferentes do que a gente está acostumado. A do primário está na parte de cima do enrolamento enquanto a do secundário está na parte inferior.
Quando isso ocorre, a gente considera a relação de transformação negativa. Então,
Passo 3
Agora, vamos referir as grandezas do primário para o secundário. A tensão do primário referida para o secundário será:
Já a resistência referida para o secundário será:
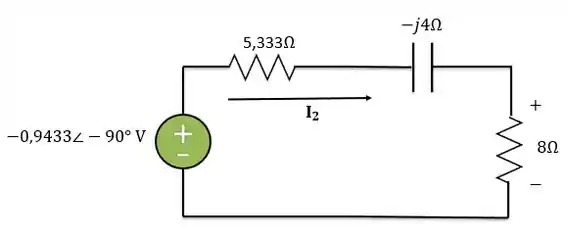
Passo 4
Agora já é possível calcular a corrente no secundário. Pela Lei de Ohm:
Passo 5
Finalmente podemos calcular a potência dissipada pelo resistor de :