Suponha que 1kg de vapor d’água saturada a 100°C seja condensado, obtendo-se líquido saturado 100°C num processo de pressão constante, através da transferência de calor para o ar ambiente que está a 25°C. Qual é o aumento líquido de entropia para o conjunto sistema e meio?

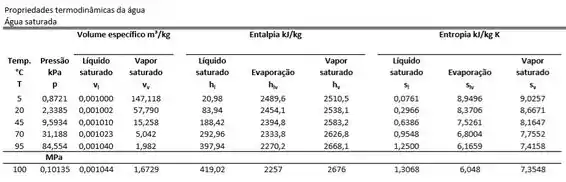
Como estamos trabalhando com os estados de vapor saturado a 100°C e líquido saturado a 100°C devemos olhar a última linha da tabela. Assim, olhando pela última linha e nas colunas da entropia para líquido saturado e vapor saturado vamos ter o valor da entropia para estes dois estados termodinâmicos. Que são respectivamente e

Como 100% da água é condensada basta subtrair os dois valores, lembrando que o resultado deverá ser negativo pois a entropia do sistema está diminuindo (o sistema na fase líquida é mais ordenado do que na fase vapor).

Aqui vale uma observação. Podemos ver que o valor achado é exatamente o oposto da entropia de vaporização. Ou seja, quando 100% da substância é vaporizada ou condensada podemos usar diretamente a propriedade com relação a vaporização, ao invés de subtrair as duas.

Continuando, aqui estamos falando da entropia específica. Para acharmos a entropia total devemos multiplicar isso pela massa fornecida no problema de 1 kg.

Repare agora que a unidade não possui mais a massa no denominador. Aqui achamos a variação de entropia para o sistema.

Agora vamos achar a variação da entropia no meio. Para isso vamos utilizar a equação do aumento de entropia no meio

Já sabemos que a temperatura de transferência de calor é de 25°C. Agora temos de saber a quantidade de calor trocado.

Como o processo foi isobárico então a quantidade de calor transferido é igual a variação da entalpia do sistema. Portanto, pela tabela e utilizando o mesmo pensamento do passo 3, temos que

Agora substituímos na equação, lembrando que a temperatura deve estar em Kelvin

O aumento líquido da entropia será igual à soma dos dois

Isso faz sentido pelo princípio do aumento da entropia!