Teoria
Entropia
A entropia pode ser associada ao grau de desordem de um sistema, mas como que vamos calcular o valor da entropia?
Lembra que a entropia é uma propriedade? Claro né! Então ela não vai depender do caminho, se é reversível ou irreversível, porque uma propriedade depende apenas do ponto final.

Para a situação de um ciclo reversível temos que
Logo, a integral é a mesma para todos os caminhos reversíveis. Assim a entropia será definida como
Onde é uma variação infinitesimal da entropia, uma variação infinitesimal do calor (oberseve que utilizamos esse delta diferente porque o calor depende do caminho, enquanto a entropia não) e a temperatura na qual toda essa desgraça acontece!
No caso de um processo irreversível
É importante notar que a entropia é definida segundo caminhos reversíveis, porém como todas as propriedades, depende apenas do ponto inicial e final. Assim, um determinado estado terá sempre a mesma entropia!

A variação da entropia pode ser calculada da seguinte forma, nesse caso deve-se utilizar um caminho reversível, porque a igualdade só existe no caso reversível (se fosse irreversível seria uma desigualdade e não teria como saber o valor exato). Além disso, vimos que a entropia não depende do processo (caminho) e sim dos pontos inicial e final.
Ao integrar dos dois lados vamos ter
Vamos fazer um exemplo que simplifique tudo isso!
Exemplo
Abaixo está representado um ciclo gerador de potência. Vamos ver se este ciclo obedece à desigualdade de Clausius.
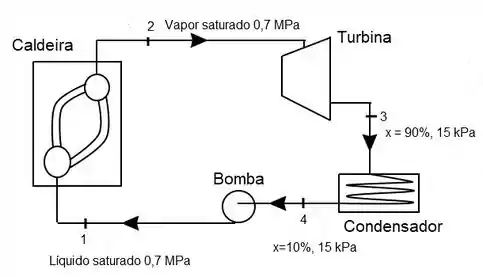
A desigualdade é dada por
Logo temos que calcular a integral cíclica da troca de calor pela temperatura. Como só há troca de calor na caldeira e no condensador podemos escrever a integral da seguinte forma
Como a temperatura é constante, tanto na caldeira quanto no condensador, podemos retira-la de dentro da integral.
Como todas as propriedades em 1 e 3 estão definidas podemos achar, pela tabela de saturação da água, as temperaturas e que são respectivamente 164,97°C e 53,97°C.
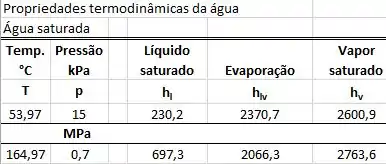
Além disso precisamos agora do calor trocado, neste exemplo podemos utilizar a quantidade de calor pela massa que é igual a variação da entalpia (que também é dada na tabela de saturação da água) entre os equipamentos, portanto:
As entalpias dos estados 1 e 2 são iguais, respectivamente, a entalpia do líquido saturado e do vapor saturado ambos a temperatura de 164,97°C.
Agora se segura e presta atenção!

Para calcular as entalpias dos estados 3 e 4 precisamos utilizar a equação:
Onde é a entalpia do líquido saturado, a entalpia de vaporação e o título:
Substituindo e lembrando que temos que utilizar a temperatura em kelvin (somar 273):
Logo, como a desigualdade resultou num valor negativo temos que ela foi satisfeita e trata-se de um ciclo irreversível.
Uma importante observação é o fato de termos utilizado a quantidade de calor específico , ao invés do calor absoluto. Isso pode ser feito porque como a massa é sempre positiva e, portanto, não alteraria a avaliação final do problema. Mas para ser rigorosamente correto deve-se multiplicar o resultado final à massa fornecida no problema, como neste caso não era necessário a massa também não foi fornecida.
Princípio do aumento da Entropia
Vimos que a entropia, diferentemente das outras propriedades, é definida por uma desigualdade para processos reversíveis. Observando que a variação de entropia para um sistema é
E para o meio será igual a
Isso acontece porque o calor trocado com o meio tem o sinal trocado em relação ao do sistema, o que sai de um entra no outro e vice-versa, além disso as irreversibilidades se encontram no sistema e não no meio. Por isso há uma igualdade ao invés de uma inequação.
Ao somarmos essas duas equações obtemos
Portanto, a entropia total do sistema + o meio terá sempre uma variação positiva para processos irreversíveis ou zero para processos reversíveis. Nunca podendo ser negativa!
Exemplo
Princípio do aumento da Entropia
Exercícios Resolvidos
Exercício Resolvido #1
Formulação própria
Explique porque muitas vezes as pessoas falam que a entropia só tende a aumentar. Isso é sempre verdade?
Passo 1
A entropia é uma propriedade da substância e, dependendo do estado desta substância, a entropia pode ser maior ou menor. Ou seja, a entropia de um sistema pode sim diminuir.
Porém para que ocorra essa diminuição algo deve ocorrer nesse sistema, como por exemplo perder calor ou realizar trabalho, com isso o meio externo ou ganha calor ou ganha trabalho, recebendo assim energia de uma forma ou de outra.
Passo 2
Quando falamos de entropia líquida ou global, estamos falando da soma da variação da entropia do meio com o sistema. Nesse caso a entropia realmente tende apenas a aumentar ou, no caso de processos reversíveis, se manter constante. Isso ocorre por causa da desigualdade de Clausius.
Resposta
A entropia líquida ou global tende apenas a aumentar ou se manter constante, isso ocorre por causa da desigualdade de Clausius.
A entropia é uma propriedade da substância e, dependendo do estado desta substância, a entropia pode ser maior ou menor.
Exercício Resolvido #2
Elaboração própria
Um copo d’água, com 200 gramas de água líquida, é aquecido da temperatura de 20°C até a temperatura de 80°C por meio de uma fonte de calor que se encontra a 600K. Sabendo que a entropia da água a 20°C era de e ao final do aquecimento a entropia era de . Calcule a irreversibilidade deste processo, ou seja, a quantidade de entropia gerada. Dado:
Passo 1
Para resolver essa questão temos de lembrar que a variação da entropia é dada pela desigualdade de Clausius na forma:
Onde, no caso reversível, vamos ter
Podemos ainda considerar que para o caso irreversível teremos:
Passo 2
Agora basta substituir os valores na equação e para isso calcular a quantidade de calor que a água recebeu
Passo 3
Substituindo
Resposta
Exercício Resolvido #3
Elaboração própria
Os equipamentos como, bombas e turbinas, são equipamentos que funcionam através de ciclos isentrópicos. Contudo, em sistemas reais é muito difícil haver de fato processos isentrópicos. Com este conceito em mente o termo eficiência isentrópica é aplicado a tais processos reais e definido como:
Com isso em mente, responda.
a) Qual a eficiência isentrópica de uma turbina ideal?
b) Um fluido possui entalpia igual a na entrada de um turbina e na saída. Sabendo que essa turbina, trabalhando num processo isentrópico, gera um trabalho específico de . Calcule a eficiência isentrópica da turbina no processo irreversível.
Passo 1
A letra “a” pede a eficiência isentrópica de uma turbina ideal, ou seja, de um processo isentrópico, de um processo reversível. Temos, portanto, que o trabalho real e ideal são iguais:
Passo 2
Na letra “b” devemos lembrar que, em turbinas e bombas, a variação da entalpia é igual ao trabalho, logo:
Não precisamos nos preocupar muito com o sinal, desde que lembremos que esse é um trabalho que sai do sistema!
O problema também forneceu o trabalho ideal da turbina
Passo 3
Basta aplicar a fórmula
Resposta
a)
b)
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.195 – Exemplo 7.13 (Adaptada).
Uma turbina é alimentada com vapor d’água que possui entalpia de igual a 3051,2 kJ/kg. Sabendo que se a transformação fosse isentrópica o vapor sairia da turbina com entalpia igual a 2309,3 kJ/kg, qual será a eficiência isentrópica desta turbina? Considerando que o trabalho produzido pela turbina foi determinado, obtendo-se o valor de 600 kJ/kg de vapor que escoa na turbina. Dica: A eficiência isentrópica de uma turbina é a relação entre o trabalho real realizado pelo trabalho que seria realizado num processo isentrópico de fato.
Passo 1
Como a própria dica do problema já nos forneceu temos que a eficiência isentrópica da turbina é uma relação entre o trabalho real e o trabalho ideal.
Com isso, vamos dizer que o trabalho real seja dado por e o trabalho ideal por , logo a eficiência isentrópica será dada por
O problema já nos forneceu o trabalho real . Portanto, precisamos calcular apenas o .
Passo 2
Para calcular o trabalho que seria realizado num processo isentrópico vamos supor que o processo é de fato isentrópico. Sendo assim não há variação de entropia e nem calor sendo trocado (porque uma transformação isentrópica é uma transformação adiabática reversível) e pela primeira lei da termodinâmica temos que:
Como a entalpia de entrada e de saída foram fornecidas o trabalho ideal é igual a diferença entre ela
Passo 3
Agora basta substituir na equação da eficiência isentrópica
Resposta
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.192 – Exemplo 7.12 (adaptado)
Calcule o trabalho, por quilograma, para bombear água isoentropicamente de 100 kPa e 30°C até 5 MPa, sabendo que o volume específico nessas condições é igual a 0,0001004 m³/kg.
Passo 1
Como trata-se de um processo reversível e em regime permanente e sem variações de energia cinético ou potencial. Podemos utilizar a relação
Podemos fazer isso porque esse trabalho é um trabalho de fluxo, logo ao invés de haver uma variação no volume do sistema, ocorre uma variação na pressão (no caso do volume de controle). Com isso a integral muda de para
Passo 2
Agora basta calcularmos essa integral
O sinal de menos na frente se justifica porque esse trabalho calculado seria o realizado pelo sistema, por isso negativo.
Portanto o trabalho para bombear a água é de .
Resposta
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.197 – Ex 7.3.
Considere um motor térmico de Carnot que utiliza água como fluido de trabalho. A temperatura do reservatório térmico onde se transfere é de 250°C. Neste processo de transferência de calor, a água se transforma de líquido saturado para vapor saturado. Sabendo que a pressão na água é igual a 100 kPa no processo de rejeição de calor, determine , a eficiência do ciclo, os calores transferidos no ciclo e a entropia da água no início da rejeição de calor para a fonte fria.
Passo 1
Vamos lá! Esse problema trata de um ciclo de Carnot e são fornecidos os seguintes dados
- Temperatura trocada na fonte quente.
- A transferência de calor na fonte quente faz com que a água passe de líquido saturado para vapor saturado. Portanto, podemos tirar diversos informações pela tabela.
- A rejeição de calor é feita a 100 kPa.
O problema pede , , , e durante a rejeição de calor.
Passo 2
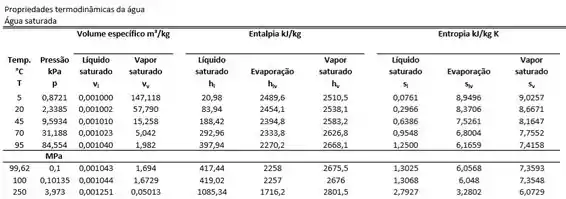
Primeiro e mais fácil vamos achar . Basta olhar na tabela qual a temperatura da água saturada a 100 kPa ou 0,1 MPa. Pela tabela vemos que esse valor é de 99,62°C
Passo 3
Como o ciclo opera segundo um ciclo de Carnot basta utilizarmos a equação da eficiência para ciclos de Carnot segundo a temperatura
Passo 4
Os calores transferidos no ciclo são iguais as variações de entalpia, isso porque são transformações isobáricas. Portanto basta usar os valor de de 250°C para o .
Para o cálculo de podemos utilizar a relação
Passo 5
Para achar o valor da entropia novamente devemos recorrer à tabela. No início da rejeição de calor temos vapor d’água a 250°C, portanto sua entropia vale
Resposta
Exercício Resolvido #7
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.168 – Exemplo 7.1.
Consideremos um cilindro provido de êmbolo, contendo vapor saturado de R-134a a -5°C. O vapor é comprimido, segundo um processo adiabático reversível, até a pressão de 1,0MPa. Determine o trabalho específico neste processo. Dados do vapor saturado a -5°C: ; ; Dados a pressão de 1,0MPa: ; ; .
Passo 1
O problema pede o trabalho específico (trabalho por unidade de massa) da transformação adiabática reversível. Então faz sentido pensar na primeira lei da termodinâmica
Que pode ser escrita da forma específica
Agora podemos ver que ao se tratar de uma transformação adiabática a quantidade de trabalho será igual a menos a variação da energia interna.
Passo 2
Como a energia interna é uma propriedade da substância basta calcular o valor dela nos pontos finais e iniciais
Isso pode ser feito através dos dados fornecidos no problema (que também poderiam ser fornecidos na forma de uma tabela), da forma
Aqui vale uma importante informação. Caso o problema fornecesse a tabela ao invés dos dados seria necessário lembrar que por se tratar de uma transformação adiabática reversível, e portanto isentrópica, não há variação da entropia. Por isso conhecemos ambos os estados dessa substância
Passo 3
Agora basta subtrair os dois valores
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.168 – Adaptado.
Ache o valor de para o vapor d’água a 10 MPa para uma mudança de fase que ocorre a pressão constante. Onde é diferença entre a entropia do vapor saturado e do líquido saturado . Dados da água saturada a 10MPa: =1317,1kJ/kg; =311,06°C
Passo 1
O próprio problema já nos fornece um dica ao falar que se trata de uma diferença entre entropias. Então vamos lembrar da equação para cálculo da entropia
Como o problema fala sobre a entropia específica, devemos dividir tudo pela massa. (Lembre-se que quando falamos de uma propriedade específica basta utilizar a letra minúscula).
Passo 2
Como não há variação de massa e nem da temperatura, porque é uma mudança de fase a pressão constante. Podemos tirar e de dentro da integral
Podemos substituir também o calor e a massa pelo calor pela unidade de massa (minúsculo).
Passo 3
Como trata-se de um processo isobárico temos que o calor transferido pela unidade de massa é igual a diferença de entalpia específica.
Como o estado 1 é o estado de líquido saturado e 2 de vapor saturado temos
É importante lembrar que a temperatura deve estar em Kelvin!
Resposta
Exercício Resolvido #9
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.174 – Exemplo 7.2.
Suponha que 1kg de vapor d’água saturada a 100°C seja condensado, obtendo-se líquido saturado 100°C num processo de pressão constante, através da transferência de calor para o ar ambiente que está a 25°C. Qual é o aumento líquido de entropia para o conjunto sistema e meio?
Passo 1
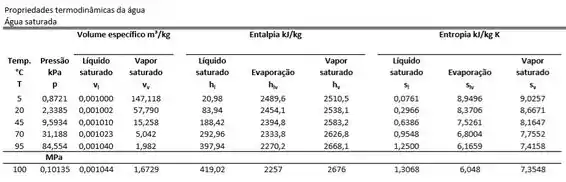
O problema pede o aumento da entropia tanto para o sistema quanto para o meio. Vamos começar pelo sistema que é mais fácil. É mais fácil porque a tabela de saturação da água nos foi dada, como a entropia é uma propriedade da substância ela tem um dado valor para cada estado.
Passo 2
Como estamos trabalhando com os estados de vapor saturado a 100°C e líquido saturado a 100°C devemos olhar a última linha da tabela. Assim, olhando pela última linha e nas colunas da entropia para líquido saturado e vapor saturado vamos ter o valor da entropia para estes dois estados termodinâmicos. Que são respectivamente e
Passo 3
Como 100% da água é condensada basta subtrair os dois valores, lembrando que o resultado deverá ser negativo pois a entropia do sistema está diminuindo (o sistema na fase líquida é mais ordenado do que na fase vapor).
Aqui vale uma observação. Podemos ver que o valor achado é exatamente o oposto da entropia de vaporização. Ou seja, quando 100% da substância é vaporizada ou condensada podemos usar diretamente a propriedade com relação a vaporização, ao invés de subtrair as duas.
Continuando, aqui estamos falando da entropia específica. Para acharmos a entropia total devemos multiplicar isso pela massa fornecida no problema de 1 kg.
Repare agora que a unidade não possui mais a massa no denominador. Aqui achamos a variação de entropia para o sistema.
Passo 4
Agora vamos achar a variação da entropia no meio. Para isso vamos utilizar a equação do aumento de entropia no meio
Já sabemos que a temperatura de transferência de calor é de 25°C. Agora temos de saber a quantidade de calor trocado.
Passo 5
Como o processo foi isobárico então a quantidade de calor transferido é igual a variação da entalpia do sistema. Portanto, pela tabela e utilizando o mesmo pensamento do passo 3, temos que
Passo 6
Agora substituímos na equação, lembrando que a temperatura deve estar em Kelvin
Passo 7
O aumento líquido da entropia será igual à soma dos dois
Isso faz sentido pelo princípio do aumento da entropia!
Resposta
Exercício Resolvido #10
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.197 – Exercício 7.9.
Um conjunto cilindro-pistão contém amônia que inicialmente está a 50°C e 1 MPa. A amônia é, então, expandida num processo adiabático reversível até que a pressão atinja 100 kPa. Determine o trabalho realizado e o calor transferido neste processo.
Passo 1
O problema pede o trabalho realizado e o calor transferido no processo. A primeira coisa é perceber que se trata de uma adiabática, portanto, o calor trocado é igual a zero. A partir daí vamos utilizar a 1ª Lei da termodinâmica para achar o trabalho:
Como o calor é zero
Passo 2
Agora fica claro que se acharmos a variação da energia interna então teremos o resultado do problema, o trabalho. Vamos ter que utilizar a tabela termodinâmica da amônia para encontrar os dois estados termodinâmicos (o primeiro já está dado) e calcular a energia interna.
O primeiro estado é amônia a 50°C e 1 MPa, ou seja, trata-se de vapor superaquecido e pela tabela temos os seguintes dados:
Perceba que a energia interna não é dada, mas pode ser calculada através da relação entre energia interna e entalpia da forma:
Como trata-se de 1kg de amônia:
Viu que quando temos 1kg então podemos passar direto de para , isso vale para todas as outras propriedades.
Passo 3
Então só falta achar para resolvermos o problema. A pressão já foi dada e é igual a 100 kPa. Precisamos de mais um dado para achar o estado, esse dado vem do fato de ser uma isentrópica, ou seja,
Para que a amônia esteja com pressão de 100 kPa e entropia de 5,2654 kJ/(kg K) é necessário que ela esteja no estado de saturação, então olhando a tabela de saturação temos uma pequena decepção a pressão de 100 kPa não consta diretamente na tabela. Logo, vamos ter que fazer novamente uma interpolação entre as pressões de 97,98 kPa e 108,29 kPa. Vamos ter que fazer essa interpolação para achar:
Que saco né? Mas é o jeito porque a tabela está em função da temperatura e não da pressão (que nesse caso provavelmente o valor de 100 kPa seria dado diretamente).
Então vamos começar para . Lembrando que o objetivo aqui agora é achar o título.
Agora para
Reparou que o lado esquerdo sempre vai aparecer o 3,84 (porque depende das pressões que são sempre as mesmas), isso agiliza o processo um pouco. Então olha como dá para fazer para
Passo 4
Vamos continuar fazendo os cálculos do passo 3 mas dessa forma um pouco mais ágil. Para :
Para
Para
Passo 5
Vamos calcular o título, entalpia e volume específico do estado 2, utilizando sempre a relação da forma:
O título:
A entalpia
O volume específico
Passo 6
Vamos utilizar a relação para achar a energia interna:
Passo 7
Como