Faça um programa para gerar os n primeiros termos da seqüência:
Passo 1
A sequência mostrada na questão é conhecida como Sequência Fibonacci, e é muito importante no estudo das ciências naturais, como a física e a biologia. Nessa sequência o primeiro termo é e o segundo termo é . E daí por diante, cada número é a soma dos dois números anteriores. Ou seja, a sequência é dada pela relação:
Então, vamos lá declarar nossas variáveis.
Como usaremos um loop vamos precisar de uma variável de iteração . Também será necessária uma variável inteira para receber o número de termos que o usuário quer imprimir.
Para efetuar a Sequência Fibonacci vamos precisar de três variáveis: para representar o termo . A variável para representar o termo . E a variável para representar o termo .

Passo 2
Pra começar, vamos usar o para pedir um número pro usuário, e com vamos armazenar o valor na variável
![]()
Passo 3
Agora vamos criar o nosso loop
O primeiro termo da sequência ocorre em
![]()
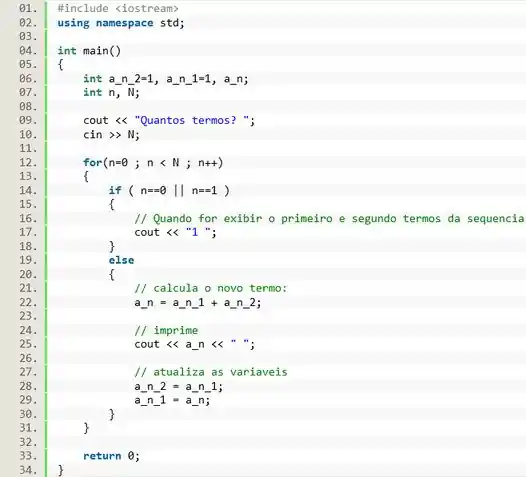
Saca só, quando e , nós não precisamos fazer nenhum cálculo. Só temos que imprimir os termos e , então podemos usar uma condição para esses casos especiais

Show! E pra todas as outras possibilidades a gente vai efetuar o cálculo. Então abrimos um comando , assim todos os outros termos da sequência, que não vão entrar no da linha 14, vão entrar no . Dentro do , na linha 22, adicionamos a expressão a expressão pra calcular o próximo termo. E na linha 25, imprimimos o valor desse novo termo.

Ainda dentro do , vamos ter que atualizar os valores das variáveis e a_n_2, para podermos calcular o próximo . O valor contido em será enviado pra ; e o valor de será enviado pra . Isso é necessário para preparar os as variáveis para a próxima iteração do laço! Olha só como fica:
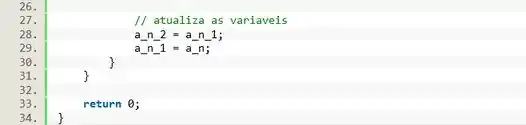
E pronto! Depois de fechar as chaves do e do laço a questão está concluída.
Resposta