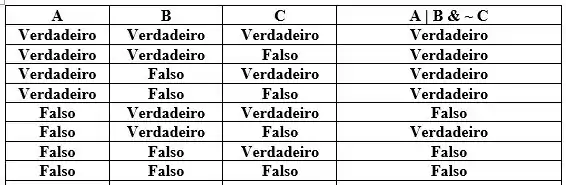
Complete a tabela verdade utilizando a tabela lógica do Matlab.
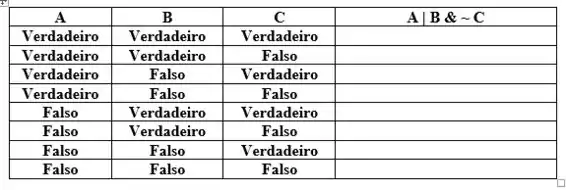
Passo 1
Essa é uma questão comum da construção de tabela verdade, para isso precisamos nos lembrar principalmente da tabela de procedência, pois para qualquer questão de tabela verdade que você irá responder precisa saber a ordem da resolução das operações.
A ideia aqui é como na matemática elementar, primeiramente em uma equação se resolve os produtos e divisões e por último as somas e subtrações, esse fenômeno é chamado de precedência e é essa informação que precisamos primeiramente entender.
A tabela de precedência do teste lógico é a seguinte:
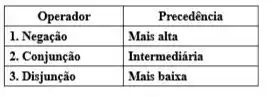
Logo, para resolver qualquer questão de teste lógico precisamos sempre resolver primeiro as expressões de Negação, seguida das conjunções e finalizaremos com a disjunção. Agora que sabemos disso iremos precisar lembrar do que cada operação dessa faz.
Para isso precisaremos de uma outra tabela, que é essa aqui:

E devemos nos lembrar que a negação é sempre a resposta contrária do que está perguntando.
A conjunção lógica só gera um resultado verdadeiro em uma única situação, que é quando ambas as entradas do teste lógico são verdadeiras. As demais situações são falsas.
E a disjunção lógica só dá uma saída falsa quando ambas as entradas do teste lógico são falsas. Os demais casos são verdadeiros.
Esses mnemônicos são úteis para memorizar essas regrinhas dos testes lógicos para você poder aplicar eles direitinho nas provas.
Agora que sabemos disso, vamos lá.
Passo 2
Então vamos lá, vamos começar a resolver!
Como vimos no passo anterior, a prioridade mais alta é a negação, então começamos com ela. A tabela de negação é o contrário da coluna C, lembrando disso temos que o que for verdadeiro se torna falso e o que for falso irá se tornar verdadeiro, belezinha?

Passo 3
A conjunção ( ) é de procedência intermediária, então ela é resolvida como a segunda operação. Na conjunção, a saída de dados só é verdadeiro se ambas as entradas são verdadeiros, ou seja, precisamos que seja verdadeiro e seja verdadeiro para que retorne uma saída verdadeira. Qualquer caso contrário a isso gera uma saída falsa.

Passo 4
E agora para finalizar precisamos apenas fazer a disjunção lógica, que representa o prefixo OU. No operador lógico OU, a resposta é falsa em uma única condição, que é o caso em que as variáveis lógicas de entrada são ambas falsas, ou seja, tanto o quanto o precisam ser ambos falsos.
Se pelo menos uma das entradas for verdadeira (seja apenas 1 ou ambas) a resposta é Verdadeira, logo:
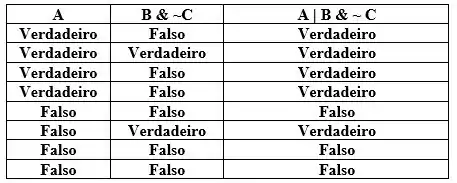
EEEEEEEEEEEEE AGORA SIIIIIM FINALIZAMOS
Resposta