Expressões Aritméticas, Relacionais e Lógicas
Produzido por Gustavo BarbosaTeoria
E lá vamos nós, mais definições....
Iae jovem, está tudo joinha?
Espero que sim, pois hoje iniciaremos mais uma magnífica conversinha sobre programação em Matlab.

Até o momento estávamos aprendendo definições básicas como inserir variáveis, algumas regrinhas de como inseri-las e, até seus tipos, mas hoje começaremos a operá-las e para isso precisamos entender o que é uma expressão.
Os livros costumam definir uma expressão como sendo uma combinação de itens sintáticos, que podem consistir de uma constante, uma única variável, de um único elemento de matriz, ou mesmo de uma combinação de constantes unidos com um ou mais operadores.
Bem, assim como eu quando li isso pela primeira vez a sua cabeça deve estar algo do tipo, “an?”

MAAAAAAAAAAS não precisa entrar em desespero, de uma forma prática uma expressão é algo até deboas de entender, olha só, imagina que você foi no mercado querendo comprar banana e o vendedor te aponta as laranjas, aí na sua cabeça vem logo:
Seu cérebro: Não!
Logo, intuitivamente seu cérebro montou uma expressão, você associou dois elementos por um operador chamado de igualdade.
Generalizando esse exemplo, uma expressão pode ser vista como uma associação de variáveis através de algum operador. E são esses operadores que iremos estudar agora!
Operadores Aritméticos
Um operador aritmético é usado para expressar uma computação numérica. Por exemplo, se o programador precisar operar uma soma ou uma igualdade como já foi mostrado nas aulas anteriores.
A sintaxe da inserção dos operadores aritméticos no Matlab é mostrada rapidinho na tabela abaixo:

Por exemplo, se quisermos executar uma operação de multiplicação, basta ir no command window e colocar:
Após isso colocar a expressão:
E rapidamente é mostrado:

Ou se caso quiser executar uma potenciação, podemos aproveitar as variáveis e e colocar, a expressão .

Você deve estar todo feliz pensando, “AHHH é só isso? Tá até tranquilo”.

Aqui não é matéria de português filho, mas pense numa coisa para existir é a tal da regra e são elas que iremos analisar agora:
Regra 1: Os parênteses podem ser utilizados para agrupar operandos em uma expressão e qualquer expressão entre parênteses tem prioridade.
Por exemplo, se você executar a expressão , primeiro ele soma e depois multiplica.
Regra 2: Com a exceção dos parênteses, as operações são realizadas por uma ordem de precedência, ou seja, existe uma ordem na execução da expressão, a tabelinha abaixo da uma ideia dessa ordem de execução.

Deve estar se passando na sua cabeça, “nossa é muita regra...”
Mas não precisa decorar tudo, se você analisar bem as regras de operação são as mesmas que utilizamos na nossa matemática básica, porém, existem uma observação importante: nos operadores de mesma ordem de precedência, o cálculo se desenvolve da esquerda para a direita
Por exemplo: . Primeiro ele vai multiplicar e depois dividir.
Expressões Relacionais
Bem galera, uma expressão relacional é utilizada para comparar os valores de duas expressões aritméticas ou de expressões com variáveis strings.
Essas comparações são realizadas pelos operadores relacionais como mostrado na tabela abaixo.
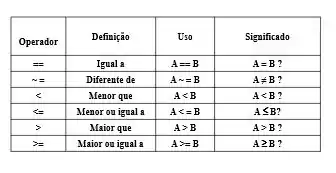
Logo, conforme a tabela acima a operação de comparação gera uma pergunta, por exemplo: é igual a ?
Para esse tipo de pergunta temos apenas duas respostas, Verdadeiro ou Falso. Logo, a saída das expressões de comparação pertence a um grupo específico de variável: as variáveis lógicas.
Vamos fazer um exemplo: no command Window, digite:
E digite a seguinte expressão conforme a tabelinha, e dê enter, deve aparecer algo do tipo:

Lembrando que para o Matlab uma variável lógica igual a 0 corresponde ao falso.
Expressões lógicas
Uffa.... Longa essa aula né?
Mas finalmente chegamos na última que é a expressão lógica.
A expressão lógica é utilizada para computação lógica. O seu cálculo produz uma variável do tipo lógico, ou seja, é verdadeiro ou falso.
Geralmente é nessa parte que a galera sente mais dificuldade, mas não se preocupe selecionamos vários exercícios para você praticar. Ahhh e antes que eu me esqueça os operadores lógicos são esses logo abaixo:

Esses operadores lógicos têm algumas observações que são pertinentes, antes do Matlab 6 esses operadores tinham a mesma precedência, porém a partir do 6 algumas regrinhas foram colocadas neles, e a precedência atual é a seguinte:
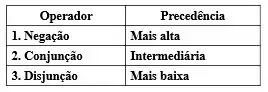
As demais regrinhas são similares às de operação aritmética, podemos mudar a precedência pela inserção dos parênteses, e uma vez que as regras acima estão ok, a execução é da esquerda para a direita.
Extras
Pra fechar, é importante falar que também existem diferentes precedências de acordo com o tipo de operadores:
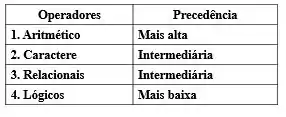
Bem galera, sabemos que o conteúdo foi extenso e cheio de detalhes, mas selecionamos uns exercícios para você treinar! E não deixe de treinar, porque programação é uma área muito mais prática que teórica. Ou seja, quanto mais você praticar, melhor irá ficar.
Bem, vamos ficar por aqui e até a próxima!!!!!!!!!! VAAAAAAAAAAALEU
Operadores Aritméticos
Expressões Relacionais
Expressões lógicas
Extras
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o valor das expressões aritméticas no Matlab. Utilize
a)
b)
c)
Passo 1
A questão pede pra gente executar as operações descritas nas alternativas, para que se possa praticar as operações aritméticas dentro do ambiente de programação Matlab.
Para a resolução de uma forma simples precisamos inserir cada variável no Matlab e após isso programar as expressões descritas nas alternativas, sendo assim o passo a passo da resolução da questão é dado pelos seguintes etapas:
Passo 2
Fala aí pessoal! O primeiro passo, é introduzir as variáveis no Matlab para que possamos utilizá-las em todas as expressões aritméticas que foi dada nas alternativas das questões, então vamos lá:
Se você digitou correto vai aparecer algo assim:
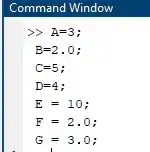
Agora que as variáveis já foram definidas dentro do ambiente Matlab, basta colocar as expressões uma de cada vez.
Passo 3
Seguindo a ordem vamos escrever a expressão da primeira alternativa que corresponde a:
Aqui não iremos precisar impor parênteses nem nada, pois a ordem de precedência da operação de divisão e multiplicação é equivalente e ambas são maiores que a soma, então primeiro o Matlab multiplica e divide e por último soma.
Sendo assim, no seu Matlab deve mostrar algo mais ou menos assim:

Passo 4
A segunda expressão tem um detalhe a considerar, a variável está multiplicando a soma , então se não colocarmos os parênteses a expressão ficaria assim:
A precedência faz com que A multiplique o B e depois que realiza a operação soma com o C, pois a precedência do produto é maior que a soma, para evitar isso precisamos colocar o parênteses na soma deixando da seguinte forma:
)
Pois o parênteses obriga o Matlab primeiramente somar e por último fazer o Matlab multiplicar a soma para o A, como a precedência da multiplicação e produto é igual não precisamos colocar o parênteses nessas operações.
Sendo assim a expressão no Matlab fica:
Sendo assim, no seu Matlab deve aparecer algo mais ou menos assim:

Passo 5
Devido às razões já mostradas nos passos anteriores, precisamos inserir os parênteses nas somas para garantir que o Matlab irá primeiramente realizar as somas e depois que irá realizar as operações de produto e divisão.
Como as operações de divisão e produto tem precedência igual, não precisamos inserir os parênteses.
Sendo assim, a expressão final fica assim:
Se você inseriu tudo certinho no Matlab, deverá aparecer algo assim para você:

Resposta
Introduzindo as expressões descrita no enunciado, você irá obter os seguintes valores como resposta:
A=41
B=99
C=441
Exercício Resolvido #2
Elaboração Própria
- Complete a tabela verdade utilizando a tabela lógica do Matlab.

Passo 1
Fala aí, galerinha! Tudo bem?
Esse exercício pede pra gente completar a tabela verdade. Tabela Verdade é uma ferramenta pra nos ajudar a encontrar o valor lógico (verdadeiro ou falso) de uma sentença, de acordo com o operador que está sendo usado e os valores lógicos das variáveis envolvidas.
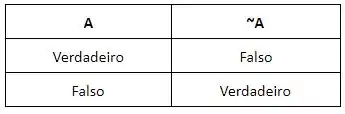
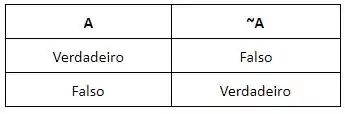
Sabemos que ~A, que aparece na tabela, é um operador lógico de negação. Esse operador é usado com apenas uma variável, e a função dele é inverter o valor lógico desta variável. Logo, se a variável é verdadeira, o resultado será falso. E se a variável é falsa, o resultado ficará verdadeiro.
Passo 2
Então vamos completar a tabela. Se A é verdadeiro, a resposta é que ~A fica falso. E se A é falso, a resposta é que ~A fica verdadeiro.
Resposta
Exercício Resolvido #3
Elaboração Própria
- Complete a tabela verdade abaixo utilizando o teste lógico que se pede na tabela.

Passo 1
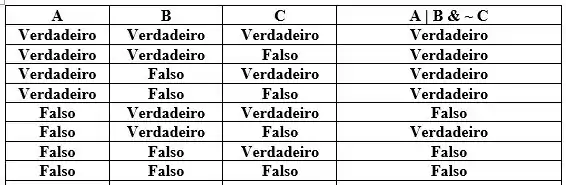
Pessoal, a ideia aqui é completar a tabela lógica, belezinha?
Olhando o prefixo A|B sabemos da teoria que ele é o operador lógico OU. Então lembrando da tabelinha do prefixo OU, se temos duas proposições e pelo menos uma delas é verdadeira, a operação A|B irá retornar como verdadeiro.
Sendo assim uma regrinha mnemônica para que você lembre rapidinho para sua prova temos que a operação A|B é verdadeiro em dois casos, como se segue abaixo:
Se A ou B é verdadeiro então A|B é verdadeiro.
Se A e B é verdadeiro então A|B é verdadeiro.
Qualquer outra proposição diferente dessas irá retornar o valor de falso.
Passo 2
Logo completando a Tabela. Na primeira linha:
Na segunda linha:
Na terceira linha:
Resposta
Sendo assim, a resposta final seria as seguintes:
Verdadeiro, Verdadeiro e Falso
Gerando a seguinte tabela:

Exercício Resolvido #4
Elaboração Própria
Escrever expressões lógicas/relacionais em Matlab que reflitam o significado das seguintes frases ou condições:
- X está no intervalo aberto (0, 10);
- X está no intervalo fechado (0, 10);
c) ;
d) ;
Passo 1
Aqui é uma questão teórica pessoal. A ideia aqui é justamente treinar as expressões e como implementá-las no Matlab, basicamente iremos responder as questões com o auxílio da seguinte tabela:

Para um entendimento e decoreba dessa tabela de uma forma mais rápida precisamos lembrar que a conjunção lógica é o E , disjunção lógica é o OU.
Uma vez que sabemos disso, precisamos apenas lembrar de mais um detalhe que o E na hora de programar é trocado pelo operador & e no caso da disjunção o OU se torna o operador |.
Passo 2
- X está no intervalo aberto (0, 10)
- X está no intervalo fechado (0, 10);
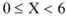
Matematicamente nós temos que o valor de X precisa ser maior do que 0 mas ele precisa ser menor do que 10, então a expressão matemática se torna:
Mas isso são duas informações e precisamos escrevê-las separadamente. Então nós temos que ele precisa obrigatoriamente ser
Então olhando a tabela de comparação e a tabela de operadores lógicos, temos que a operação E é uma conjunção lógica, então vamos trocar a letra pelo operador , sendo assim a expressão fica:
Passo 3
Esse caso é igual o anterior, só que introduz o valor igual, pois matematicamente temos que precisa ser maior ou igual a 0 e menor ou igual a 10, pois ele está no intervalo fechado de 0 até 10, ou seja, ele pode assumir qualquer valor entre o 0 e o 10.
Sendo assim a expressão se torna:
utilizando a mesma lógica da questão anterior, podemos ver que é uma conjunção lógica ou seja o E vai ser trocado pelo operador .
Passo 4
Diferente da alternativa anterior, essa aqui já nos dá a informação do intervalo, o que nós devemos fazer é quebrar o intervalo e incorporar o teste lógico.
Esse simples intervalo nos dá duas informações, a primeira informação é que o X precisa ser maior ou igual ao 0, gerando a seguinte expressão:
A segunda informação é que o precisa ser menor do que o número 6, gerando a seguinte expressão:
Como a variável X precisa estar entre esses valores então ambas as condições precisam ser satisfeitas, logo:
Caracterizando como uma conjunção lógica e trocando o E pelo operador , temos que:
Passo 3
d) ![]()
A questão nos informa que o valor de M pode assumir dois conjuntos de valores:
Aqui temos dois intervalos, e o prefixo é o de OU olhando a tabela de condição lógica, vamos que o OU é trocado pelo operador |.
Sendo assim, as expressões são escritas da seguinte forma:
Resposta
Sendo assim as respostas finais se tornam:
Exercício Resolvido #5
Elaboração Própria
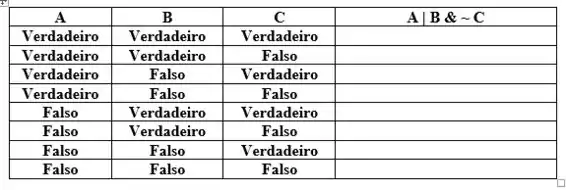
Complete a tabela verdade utilizando a tabela lógica do Matlab.
Passo 1
Essa é uma questão comum da construção de tabela verdade, para isso precisamos nos lembrar principalmente da tabela de procedência, pois para qualquer questão de tabela verdade que você irá responder precisa saber a ordem da resolução das operações.
A ideia aqui é como na matemática elementar, primeiramente em uma equação se resolve os produtos e divisões e por último as somas e subtrações, esse fenômeno é chamado de precedência e é essa informação que precisamos primeiramente entender.
A tabela de precedência do teste lógico é a seguinte:
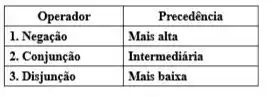
Logo, para resolver qualquer questão de teste lógico precisamos sempre resolver primeiro as expressões de Negação, seguida das conjunções e finalizaremos com a disjunção. Agora que sabemos disso iremos precisar lembrar do que cada operação dessa faz.
Para isso precisaremos de uma outra tabela, que é essa aqui:

E devemos nos lembrar que a negação é sempre a resposta contrária do que está perguntando.
A conjunção lógica só gera um resultado verdadeiro em uma única situação, que é quando ambas as entradas do teste lógico são verdadeiras. As demais situações são falsas.
E a disjunção lógica só dá uma saída falsa quando ambas as entradas do teste lógico são falsas. Os demais casos são verdadeiros.
Esses mnemônicos são úteis para memorizar essas regrinhas dos testes lógicos para você poder aplicar eles direitinho nas provas.
Agora que sabemos disso, vamos lá.
Passo 2
Então vamos lá, vamos começar a resolver!
Como vimos no passo anterior, a prioridade mais alta é a negação, então começamos com ela. A tabela de negação é o contrário da coluna C, lembrando disso temos que o que for verdadeiro se torna falso e o que for falso irá se tornar verdadeiro, belezinha?

Passo 3
A conjunção ( ) é de procedência intermediária, então ela é resolvida como a segunda operação. Na conjunção, a saída de dados só é verdadeiro se ambas as entradas são verdadeiros, ou seja, precisamos que seja verdadeiro e seja verdadeiro para que retorne uma saída verdadeira. Qualquer caso contrário a isso gera uma saída falsa.

Passo 4
E agora para finalizar precisamos apenas fazer a disjunção lógica, que representa o prefixo OU. No operador lógico OU, a resposta é falsa em uma única condição, que é o caso em que as variáveis lógicas de entrada são ambas falsas, ou seja, tanto o quanto o precisam ser ambos falsos.
Se pelo menos uma das entradas for verdadeira (seja apenas 1 ou ambas) a resposta é Verdadeira, logo:
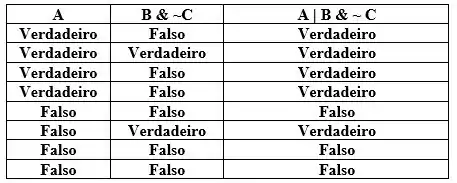
EEEEEEEEEEEEE AGORA SIIIIIM FINALIZAMOS
Resposta
Exercício Resolvido #6
Elaboração Própria
Julgue se as expressões abaixo são verdadeiras ou falsas utilizando as procedências do Matlab.
Passo 1
Essa é uma questão comum de construção de tabela verdade e para resolver essa questão iremos precisar lembrar do que cada operação dessa faz.
Para isso precisaremos de uma outra tabela, que é essa aqui:

Agora que temos as ferramentas em mão, iremos resolver a questão ok?
Passo 2
Na letra a) são dados 2 intervalos para a função sen(x): maior que -1 e menor que 1. E essas duas informações são apresentadas com o operador lógico &. Como vemos na tabela, o operador & significa E.
Então, traduzindo para o português, a alternativa está te perguntando o seguinte:
O valor do seno de x é maior do que E menor do que
Como sabemos o seno oscila nesse intervalo, então essa alternativa é verdadeira.
Passo 3
Na letra b) temos o operador == que é um operador de comparação. Traduzindo para o português nós temos a seguinte pergunta:
Tomate é igual a fruta? O tomate é uma fruta?
Como sabemos o tomate é uma fruta, porém, muitas pessoas ainda acreditam que ele é uma leguminosa. Mas, não podemos reescrever a biologia então essa também é verdadeira.
Resposta

Exercício Resolvido #7
Elaboração Própria
Em Matlab foram atribuídas as seguintes variáveis . Sendo assim qual o valor de cada uma das expressões?
Passo 1
A ideia da questão é que ela informa os valores das variáveis e pede para calcular umas expressões.
Devemos lembrar que o Matlab na hora de resolver essas expressões ele tem uma certa precedência de um determinado operador sobre outro, sendo assim, a ideia é resolver as equações e encontrar os valores conforme as regras que o Matlab usa.
Passo 2
Na alternativa a, temos a seguinte expressão:
Podemos perceber que aqui temos apenas multiplicações e divisões.
Logo, a prioridade entre esses operadores é similar. Sendo assim, as operações são feitas da esquerda para direita, logo temos que essa expressão é o mesmo que:
Passo 3
Na segunda alternativa temos a seguinte expressão:
Analisando a expressão temos a potenciação que tem a maior prioridade, ou seja, primeiramente deveríamos resolvê-la.
Porém, temos um parêntese na operação de soma, devido a isso primeiramente devemos resolver os parênteses para depois resolver o resto da expressão.
Logo, essa expressão é equivalente a:
Passo 4
E por último a terceira expressão é dada por:
As operações são as potenciações e as somas, porém, não temos os parênteses.
Logo, devemos primeiramente resolver a potenciação.
Sendo assim, a expressão tem o seguinte valor:
Passo 5
Colocando as variáveis na janela do Command Window temos que:

Comparando com os valores que calculamos manualmente vemos que todos batem perfeitamente, ou seja, executamos as precedências corretamente.
Resposta
Logo as respostas finais são:
Exercício Resolvido #8
Elaboração Própria
Quais das seguintes expressões abaixo resultam em valores lógicos verdadeiros:
Passo 1
A ideia da questão é analisar cada proposição e dizer quais delas apresentam um valor verdadeiro, ou seja, a variável logica dela da 1.
Porém, as alternativas aqui possuem algumas sutilezas que vamos conversar em cada alternativa.
Passo 2
Na alternativa a, temos a seguinte expressão:
Podemos perceber aqui que a expressão pergunta quem é maior, ou seja, pergunta se o 5.10 é maior que 10. Se for, temos uma opção verdadeira. Mas não é.
Logo, como 5.10 é menor do que 10, temos uma resposta falsa, ou seja, 0.
Passo 3
Aqui temos a seguinte expressão:
Aqui nós temos uma expressão que pergunta se o string sorvete é menor que o string açaí.
Quando nós vamos comparar o tamanho de duas palavras geralmente comparamos o número de letras, e o Matlab faz o mesmo.
Ele contabiliza e compara o número de elementos dentro do string.
Logo, como o sorvete tem mais letras que a palavra açaí, a resposta é verdadeira.
Passo 4
Aqui temos a seguinte expressão:
Uma pessoa desatenta iria somar o e após isso compararia com o valor de , porém, aqui temos uma coisa chamada precedência.
Quando estudamos expressões em Matlab vemos que uma expressão tem uma precedência maior que os demais, ou seja, nessa questão primeiramente somos obrigados a resolver a expressão lógica antes da soma.
Sendo assim, o teste lógico é ?
Como é diferente do temos que a resposta é falsa.
Resposta
Sendo assim, após essa longa análise temos que a resposta verdadeira é unicamente a alternativa b).