Uma vazão de de uma mistura aquosa contendo (em massa) de ácido acético é alimentada no primeiro estágio de um extrator de dois estágios, utilizando-se como solvente éter isopropilico contendo (em massa) de ácido acético. O solvente é alimentado a uma vazão de em fluxo cruzado em cada estágio. Se a extração ocorre a e . Determine as vazões das correntes de extrato e de rafinado que saem do extrator.

Dados:

Vamos analisar um estágio de cada vez como se estivéssemos lidando com estágios únicos, beleza? Então vamos começar olhando para o nosso primeiro estágio:

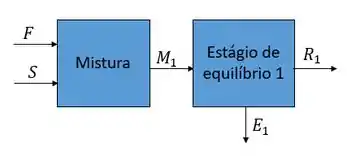
Vamos inicialmente calcular a vazão da mistura fazendo o balanço geral no misturador 1:

Com fazer um balanço global no estágio de equilíbrio 1 e encontrar,

Fazendo agora um balanço do soluto temos,

Voltando no balanço global temos,

Trabalhando agora com o segundo estágio, ou seja,

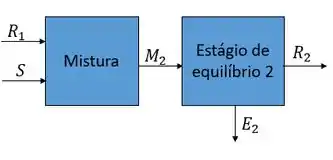
Podemos fazer o balanço global e obter,

Fazendo o balanço por componente para o soluto,

Para o diluente temos,

Para o solvente temos,

Temos que está sobre a reta e vai gerar e ao atingir o equilíbrio. Depois vamos utilizar a curva rebatendo um ponto aleatório da curva a linha conjugada obtendo,

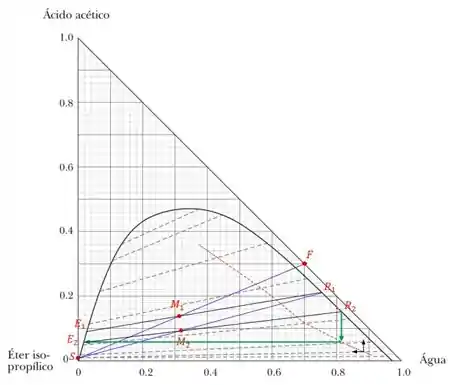
Fazendo a leitura desse gráfico vemos que a composição do extrato é,

E do rafinado é,

Agora vamos fazer um balanço global no estágio de equilíbrio 2,

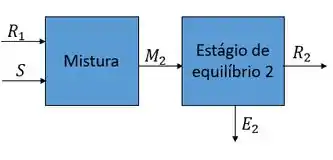
Fazendo o balanço por componente com o soluto,

Substituindo no balanço global temos,