Introdução à Condução
Produzido por Giovanna RonzéTeoria
Lei de Fourier
Tá legal, nós já vimos a Lei de Fourier antes, tudo bem... mas como estamos falando de condução, acho mais do que justo darmos uma atenção especial a ela novamente.
A Lei de Fourier não foi desenvolvida a partir de princípios fundamentais, como boa parte das leis que estudamos ao longo da graduação, ela foi desenvolvida a partir da observação de fenômenos.
Por exemplo, vamos supor que temos um paralelepípedo de um determinado material de área transversal , comprimento , e que suas extremidades possuem temperaturas fixas e .
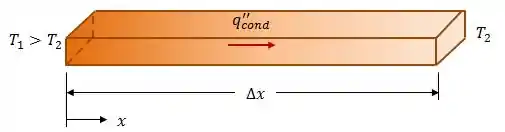
A ideia é manter duas das variáveis constantes, enquanto variamos a terceira e vemos o que acontece com a taxa de transferência de calor . Fazendo isso, vamos observar o seguinte:
- é proporcional a ;
- é proporcional a ;
- é inversamente proporcional a .
Mas tem algo muito importante aqui que ainda não falamos, que é sobre o material do nosso paralelepípedo. Se ele fosse feito de madeira, por exemplo, seria menor do que se o mesmo fosse feito de ferro, concorda?
Por isso devemos levar em consideração a condutividade térmica do material. Dessa forma, podemos escrever a taxa de transferência de calor seguinte forma:
Fazendo , chegamos a uma expressão para a Lei de Fourier:
Para o fluxo de calor por condução :
Obs.: O sinal negativo aparece porque o calor é transferido no sentido em que a temperatura diminui.
Mas o calor é transferido apenas em uma direção?!
Não necessariamente! Por isso, podemos escrever a Lei de Fourier para o fluxo de calor de uma forma mais geral, da seguinte forma:
Se liga que agora estamos tratando o fluxo de calor como uma grandeza vetorial.
Opa! Um detalhe importante é que o material onde o calor está se propagando é isotrópico, isso significa que a condutividade térmica é a mesma em todas as direções.
Raramente vai aparecer algum material que não apresente essa propriedade. Mas, se for o caso, o problema vai dizer para a gente, fica tranks.
Equação do Calor (Equação da Difusão Térmica)
Um dos principais objetivos quando analisamos a condução de calor é determinar a distribuição e temperaturas, ou seja, como a temperatura varia de ponto para ponto. Conhecida essa distribuição, podemos determinar o fluxo de calor por condução pela Lei de Fourier.
E é justamente aí que entra a Equação do Calor.
Em Mecânica dos Fluidos, a gente cansa de falar sobre conservação de massa e faz vários balanços massa, escolhendo o volume de controle adequado e tudo mais. Com a energia é o mesmo esquema.
Toda energia que entra num sistema tem que sair desse sistema, exceto nas situações em que ela vai acumulando em seu interior, ou tem algo lá dentro que consome/produz energia. Isso pode ser expresso em termos de taxa de energia :
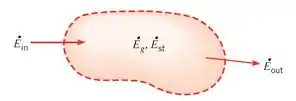
Partindo desse princípio, podemos escrever a equação acima da seguinte forma:
Pois bem, mestre, está é a Equação do Calor. Tcharaaaaaan! \o/
Nela, o termo representa a taxa de geração de energia térmica, e o termo representa o acúmulo de energia.
É importante frisar que o termo de acúmulo de energia está representando somente a energia sensível, ou seja, estamos desconsiderando mudanças de fase. Caso elas ocorram (o que é raro de aparecer) vamos ter que leva-la em consideração.
Dá pra simplificar a Equação do Calor?!
Cara, ótima pergunta! Até meio capciosa!
Então, dependendo das informações que o problema nos der, podemos fazer algumas simplificações aqui sim. Vamos dar uma olhada em algumas que aparecem direto.
- Condutividade térmica constante:
- Regime estacionário:
- Transferência de calor unidimensional, em regime estacionário e sem geração de energia:
Sendo um valor constante, nós podemos tirá-lo de cada derivada parcial e dividir toda a equação por . No final das contas, teremos o seguinte:
Aqui vamos definir uma nova grandeza, a difusividade térmica , dada por:
Onde .
“Mas porque você está falando isso agora?!”
Porque esse termo acabou de aparecer na nossa Equação do Calor, além de ser uma importante propriedade térmica.
Ela a capacidade do material de conduzir calor, em relação à sua capacidade de armazená-lo. Assim, quanto maior o valor de , mais rapidamente o material responderá a mudanças nas condições térmicas.
Voltando para a nossa equação, podemos escrevê-la da seguinte forma:
Nesse caso, , logo:
O fato da transferência de calor ser unidimensional (na direção , por exemplo) significa que temos .
Assim como acabamos de ver, o regime estacionário nos diz que .
E quando não temos geração de energia, podemos assumir que .
Dessa forma, finalmente teremos:
Condições de Contorno
Na maior parte das vezes o problema não vai nos dar as condições de contorno de um sistema já bonitinho, escrito de forma matemática. Então precisamos saber desvendar as informações que o problema der para a gente.
Basicamente, temos três tipos de condições de contorno. Vamos dar uma olhada em cada uma delas, beleza?
- Temperatura constante:
- Fluxo térmico constante:
- Convecção na superfície:
Sendo a temperatura de uma parede em constante, matematicamente, podemos escrever essa condição da seguinte forma:
Nesse caso, a temperatura se comporta da seguinte forma:
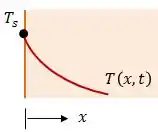
Se nessa mesma parede temos agora um fluxo térmico constante, podemos escrever que:
Graficamente, a ideia é essa:
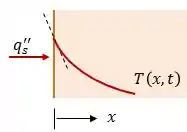
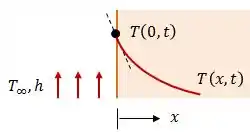
Agora, se esse fluxo térmico é nulo, dizemos então que temos uma superfície isolada termicamente ou adiabática. Esse termo é muito importante, pois ele aparece em muitas questões. Nesse caso:
E a temperatura se comporta da seguinte maneira:
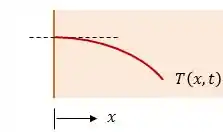
Se temos um fluido com temperatura transferindo calor por convecção para a nossa parede , podemos escrever que:
A ideia é essa:
Já temos o bastante aqui pra quebrar a cabeça nos exercícios, vamos lá!
Mas o calor é transferido apenas em uma direção?!
Equação do Calor (Equação da Difusão Térmica)
Dá pra simplificar a Equação do Calor?!
Condições de Contorno
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
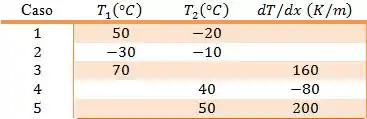
Considere condições de regime estacionário na condução unidimensional em uma parede plana com uma condutividade térmica de e uma espessura , sem geração interna de calor.

Determine o fluxo térmico e a grandeza desconhecida em cada caso e esboce a distribuição de temperaturas, indicando a direção do fluxo térmico.
Passo 1
Vamos nessa! De acordo com o problema, vamos trabalhar com o fluxo de calor por condução , dado por:
Como estamos trabalhando com a diferença de temperatura através de uma parede plana, podemos dizer que:
Se liga! Na tabela, temos que colocar como , mas o problema nos deu as temperaturas em ... como fazemos então?!
Calma! Por conta da relação entre temperaturas em Kelvin e Celsius , a variação de temperatura terá o mesmo valor, seja em graus, ou em Celsius! Então não precisamos esquentar a cabeça com isso, ok?
Além disso, teremos que determinar o sentido do fluxo térmico pra cada caso. Aqui, é importante lembrar que o fluxo térmico flui do ponto de maior temperatura para o ponto de menor temperatura.
Bom, esses conhecimentos são o suficiente pra resolver o problema. Vamos analisar, então, um caso por vez, beleza?
Passo 2
Caso 1:
Dados:
Vamos começar calculando a grandeza que falta na tabela, e depois usá-la pra calcular o fluxo de calor.
Agora estamos prontos pra calcular o fluxo de calor, dado por:
Como , o fluxo térmico vai para a direita.
Passo 3
Caso 2:
Dados:
Mesmo esquema aqui, vamos começar calculando para depois calcular o fluxo de calor, ok?
Como , o fluxo térmico fluirá para a esquerda.
Passo 4
Caso 3:
Dados:
Como o problema já nos deu , podemos calcular o fluxo de calor sem maiores problemas:
Para calcular , vamos fazer utilizar a seguinte relação:
Opa! Podemos reorganizar essa equação para encontrar :
Como , o fluxo térmico vai para a esquerda.
Passo 5
Caso 4:
Dados:
Novamente, como o problema já nos deu , podemos calcular logo o fluxo de calor:
Para calcular , vamos reorganizar a equação abaixo:
Como , o fluxo térmico fluirá para a direita.
Passo 6
Caso 5:
Dados:
Mesmo esquema do passo anterior, vamos começar calculando o fluxo de calor:
Para calcular , vamos reorganizar a equação abaixo:
Como , o fluxo térmico vai para a esquerda.
Resposta
- Caso 1:
- Caso 2:
- Caso 3:
- Caso 4:
- Caso 5:
O fluxo térmico vai para a direita.
O fluxo térmico vai para a esquerda.
O fluxo térmico vai para a esquerda.
O fluxo térmico vai para a direita.
O fluxo térmico vai para a esquerda.
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Trechos do oleoduto que atravessa o Alasca encontram-se acima do solo e são sustentados por suportes verticais de aço que possuem comprimento de e área de seção transversal de .
Em condições normais de operação, sabe-se que a variação da temperatura ao longo do comprimento do suporte é governada por uma expressão com a forma:
na qual e possuem unidades de e metros, respectivamente. Variações de temperatura na seção transversal do suporte são pequenas.
Determine a temperatura e a taxa de condução de calor na junção suporte-oleoduto e na interface suporte-solo . Explique a diferença entre as taxas de transferência de calor.
Passo 1
Vamos começar calculando a temperatura nos dois pontos que o problema pede. Como já temos a função de dada pelo problema, basta substituir os valores, beleza?
Passo 2
Agora precisamos calcular a taxa de condução de calor nesses dois pontos. Pra isso, precisamos encontrar primeiro uma expressão para .
De acordo com a Lei de Fourier:
Substituindo os valores de , e a expressão de dada pelo problema:
Passo 3
Agora estamos prontos pra calcular a taxa de condução de calor nos dois pontos:
Resposta
As taxas são diferentes pois as temperaturas estão em função da posição. Em posições diferentes as temperaturas são diferentes, logo o também é diferente e por isso as taxas não são iguais.
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Em um dado instante de tempo, a distribuição de temperaturas no interior de um corpo homogêneo infinito é dada pela função:
Considerando propriedades constantes e ausência de geração de calor no interior do corpo, determine as regiões nas quais a temperatura varia com o tempo.
Passo 1
Quem vai nos dizer como a temperatura varia as coordenadas e o tempo é a Equação de Difusão Térmica, dada por:
O problema nos disse para considerar as propriedades constantes (isso quer dizer que podemos tirar a condutividade térmica da derivada) e que não há geração de calor no interior do corpo .
Dessa forma, podemos escrever a equação acima da seguinte forma:
Agora vamos trabalhar nessas derivadas parciais!
Passo 2
Dado que a temperatura no corpo é dada por:
As primeiras derivadas serão dadas por:
E as segundas derivadas serão dadas por:
Agora podemos voltar para a Equação de Difusão de Calor.
Passo 3
Substituindo o que encontramos para as derivadas parciais, teremos:
Logo:
Isso significa que a temperatura independe do tempo em qualquer região.
Resposta
A temperatura independe do tempo em qualquer região.
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma panela é usada para ferver água. Ela é colocada sobre um fogão, a partir do qual calor é transferido a uma taxa fixa . Há dois estágios no processo.
No Estágio 1, a água é levada de sua temperatura inicial (ambiente) até o ponto de ebulição, quando calor é transferido da panela para a água por convecção natural. Durante esse estágio pode-se admitir um valor constante do coeficiente de transferência de calor , enquanto a temperatura média da água aumenta com o tempo,
No Estágio 2, a água encontra-se em ebulição e a sua temperatura mantém-se em um valor fixo, , enquanto o fornecimento de calor continua.
Considere uma base de panela com espessura e diâmetro , com um sistema de coordenadas no qual e nas superfícies em contato com o fogão e com a água, respectivamente.
Escreva a forma da equação do calor e as condições inicial e de contorno que determinam a variação da temperatura com a posição e o tempo, , na base da panela ao longo do Estágio 1. Expresse o seu resultado em termos dos parâmetros , , , e , assim como das propriedades pertinentes do material da panela.
Durante o Estágio 2 a superfície da panela em contato com a água encontra-se a uma temperatura fixa, . Escreva a forma da equação do calor e as condições de contorno que determinam a distribuição de temperaturas, , na base da panela. Expresse o seu resultado em termos dos parâmetros , , e , assim como das propriedades pertinentes do material da panela.
Passo 1
Vamos nessa, meu time! A ideia aqui é essa:
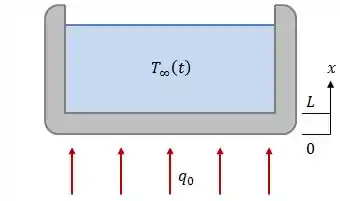
Ou seja, nos dois Estágios teremos uma taxa de transferência de calor na superfície . A única coisa que vai mudar será a condição de contorno para , que é a superfície que está em contato com a água.
Um detalhe importante aqui é que o problema nos dá a taxa de transferência de calor mas, na hora de aplicar as condições de contorno, vamos trabalhar com o fluxo de calor. Para isso, basta usar a relação:
Como o problema nos deu o diâmetro da base da panela, podemos escrever que:
Logo:
Show de bola! Agora vamos analisar cada um dos estágios, beleza?
Passo 2
Escreva a forma da equação do calor e as condições inicial e de contorno que determinam a variação da temperatura com a posição e o tempo, , na base da panela ao longo do Estágio 1. Expresse o seu resultado em termos dos parâmetros , , , e , assim como das propriedades pertinentes do material da panela.
Estágio 1
Considerações:
- Transferência de calor somente no eixo ;
- Não há geração de calor interna;
- Propriedades do material constantes;
- Fluxo de calor constante na superfície ;
- Convecção na superfície ;
- Temperatura inicial .
Começando pela Equação do Calor, temos que:
Aplicando as nossas considerações, teremos o seguinte:
Onde .
Em , temos uma condição de fluxo de calor constante, logo:
Em , temos uma condição de convecção na superfície, logo:
Pra fechar, não podemos esquecer que, inicialmente, todo o sistema está a temperatura ambiente. Sendo assim:
Pronto! Nem doeu! ;)
Vamos pro Estágio 2.
Passo 3
Durante o Estágio 2 a superfície da panela em contato com a água encontra-se a uma temperatura fixa, . Escreva a forma da equação do calor e as condições de contorno que determinam a distribuição de temperaturas, , na base da panela. Expresse o seu resultado em termos dos parâmetros , , e , assim como das propriedades pertinentes do material da panela.
Estágio 2
Considerações:
- Transferência de calor somente no eixo ;
- Não há geração de calor interna;
- Propriedades do material constantes;
- Fluxo de calor constante na superfície ;
- Temperatura constante em .
Começando pela Equação do Calor, é importante ressaltar que, como agora a temperatura está constante em , não há mais variação de temperatura com o tempo, já que a água está passando por mudança de fase, dessa forma:
Aplicando as nossas considerações, teremos o seguinte:
Em , temos uma condição de fluxo de calor constante, logo:
Em , temos uma condição de temperatura constante, logo:
Acabou! :)
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um tanque solar de gradiente salino é um corpo raso de água, composto por três camadas distintas de fluidos, que é usado para coletar energia solar.
As camadas externas superior e inferior encontram-se bem misturadas e servem para manter as superfícies superior e inferior da camada intermediária em temperaturas uniformes e , onde . Embora exista movimentação do fluido nas camadas misturadas, tal movimento não está presente na camada central.
Considere condições nas quais a absorção de radiação solar na camada central implique em geração de calor não-uniforme na forma e a distribuição de temperaturas nessa camada seja:
As grandezas , , e são constantes conhecidas que possuem as unidades indicadas e é a condutividade térmica, que também é constante.
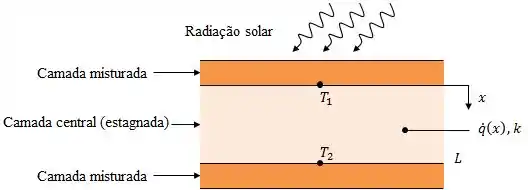
Obtenha expressões para a taxa, por unidade de área, na qual o calor é transferido da camada inferior misturada para a camada central e da camada central para a camada superior misturada.
Determine se as condições do sistema são de regime estacionário ou de regime transiente.
Obtenha uma expressão para a taxa na qual a energia térmica é gerada em toda camada central, por unidade de área superficial.
Passo 1
Obtenha expressões para a taxa, por unidade de área, na qual o calor é transferido da camada inferior misturada para a camada central e da camada central para a camada superior misturada.
Quando o problema pede a taxa por unidade de área, ele está tentando dizer educadamente que quer que a gente determine a bagaça do fluxo de calor, show?
Graficamente, como , a ideia é a seguinte:
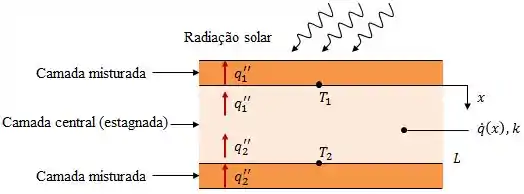
Se o problema já nos disse como a temperatura varia com o valor de , podemos começar calculando o fluxo de calor por condução:
Agora basta calcular o fluxo de calor nas duas superfícies e acabou o problema (pelo menos essa parte):
Passo 2
Determine se as condições do sistema são de regime estacionário ou de regime transiente.
Para resolver o problema, precisamos analisar a Equação do Calor e observar se:
- : Regime estacionário;
- : Regime transiente.
Vamos lá:
Aqui, vamos fazer as seguintes considerações:
- Transferência de calor somente na direção ;
- Condutividade térmica constante.
Aplicando essas condições na Equação do Calor (onde ), teremos:
O último trabalho que teremos aqui é calcular a segunda derivada :
Substituindo na expressão na Equação do Calor, teremos:
Dessa forma, as condições do sistema são de regime estacionário.
Passo 3
Obtenha uma expressão para a taxa na qual a energia térmica é gerada em toda camada central, por unidade de área superficial.
Novamente, como o problema está pedindo a taxa de energia térmica por unidade de área, o que ele quer que a gente calcule é o fluxo de energia térmica gerada. Este fluxo de energia pode ser calculado da seguinte forma:
Substituindo a expressão de , teremos:
Arrumando a casa, teremos o seguinte:

Resposta
As condições do sistema são de regime estacionário.
Exercício Resolvido #6
Questão 2, PUCRIO, P1-2003
(Adaptada) Considere o problema de condução unidimensional numa parede plana de largura e altura , com uma extremidade isolada e a outra mantida a temperatura igual a .
A parede tem condutividade térmica igual a , e no seu interior passa uma resistência elétrica que gera calor uniformemente a uma taxa de .
Escreva a equação de condução de calor e as condições de contorno apropriadas para essa situação. Em seguida, obtenha a distribuição de temperatura ao longo da parede e desenhe um gráfico (qualitativo) da temperatura x distância para a situação analisada.
Passo 1
A equação de calor é dada por:
Sabendo que a condução é unidimensional e supondo regime permanente, teremos:
Além disso, supondo que as propriedades do material sejam as mesmas em qualquer ponto da placa, teremos:
O problema nos disse que uma extremidade da placa é isolada termicamente, e a outra mantida a temperatura igual a .
Assim, as condições de contorno serão:
Passo 2
Resolvendo a equação diferencial que encontramos, teremos:
Integrando a equação em :
Aplicando a condição de contorno de superfície isolada termicamente, teremos:
Integrando novamente em :
Aplicando a condição de contorno de temperatura constante:
Assim, a distribuição de temperatura será dada por:
Passo 3
Pra analisar esse perfil de forma qualitativa, vamos dar uma olhada na função que descreve a temperatura. A temperatura é uma função de segundo grau em relação a , então será uma parábola. Como o termo do é negativo, a concavidade é para baixo.
Podemos fazer uma análise mais quantitativa, já que sabemos que, em , na extremidade da parede, .
Um esboço de versus pode ser feito assim:
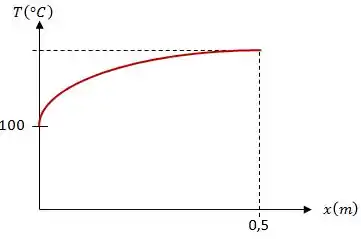
Resposta
Equação de calor:
Distribuição de temperatura:
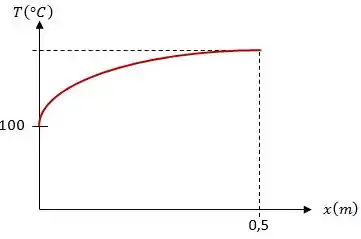
Exercício Resolvido #7
Questão 1, UFF, P1-2016.1
Uma placa plana de vidro muito fina está inicialmente à temperatura de quando é retirada de um forno. Nesse instante inicial ar é soprado paralelamente à placa produzindo um coeficiente de película para convecção .
Para que o vidro não quebre é necessário limitar o gradiente de temperatura no interior da placa a durante o processo de resfriamento.
Determine qual a temperatura mais baixa que o ar pode ter no início do resfriamento para que o vidro não quebre nesse instante inicial.
Passo 1
Aplicando o balanço de energia na placa de vidro, temos que:
Como não há geração ou acúmulo de energia, podemos escrever a equação acima da seguinte forma:
Sabendo que o calor é retirado da placa por convecção, temos que:
Reorganizando a equação acima para isolara a temperatura do ar teremos:
Passo 2
De acordo com a tabela A.3 do Incropera, a condutividade térmica do vidro será:
Além disso, de acordo com o enunciado, temos que:
Dessa forma, a temperatura mínima do ar deve ser:
Resposta
Exercício Resolvido #8
Questão 5, UFRJ, P1-2008.1
Considere condução de calor transiente e uni-dimensional em uma placa plana com propriedades constantes e espessura . A placa, que encontra-se inicialmente na temperatura uniforme , tem suas superfícies em e mantidas nas temperaturas constantes e , respectivamente.
Calor é gerado uniformemente na placa a uma taxa . Para este problema, forneça a formulação matemática.
Passo 1
A partir da equação de calor, temos que:
Vamos fazer as seguintes considerações:
- Condução de calor unidimensional;
- Condução transiente;
- Propriedades constantes.
Assim, a equação de calor pode ser escrita da seguinte forma:
Passo 2
Para condição inicial, o problema nos disse que:
Passo 3
Como condições de contorno, o problema nos disse que as superfícies em e mantidas nas temperaturas constantes e , respectivamente.
Assim:
![]()
![]()
Resposta
Exercício Resolvido #9
Questão 2, UFRJ, P1-2007.1
Uma placa de cobre com de espessura, de comprimento e de largura encontra-se na posição horizontal. Sua superfície superior é aquecida pelo sol e troca calor com o ar por convecção. A taxa de radiação solar absorvida pela placa é de .
A superfície inferior da placa troca calor por convecção com o ar. Os coeficientes de transferência de calor entre o ar e as superfícies superior e inferior da placa são e , respectivamente.
Determine a temperatura da placa no equilíbrio, sabendo a temperatura do ar é . Suponha que gradientes de temperatura na placa possam ser desprezados.
Passo 1
No equilíbrio , fazendo o balando de energia na placa, temos que:
Nesse caso, temos calor entrando na placa através da radiação solar, e o calor está saindo da placa por convecção tanto na superfície superior, quanto na superfície inferior. Logo:
Passo 2
Substituindo os valores, teremos:
Perceba que utilizamos os valores de em mesmo o valor de estando em . Isso acontece porque diferenças de temperatura são equivalentes nas duas escalas. Vamos fazer em só pra você ficar ligado.
Resposta
Exercício Resolvido #10
Questão 1, UFRJ, P1-2005.2
Um chip, com base quadrada de lado , é montado em um substrato. O substrato comporta-se como um isolante ideal. O chip é resfriado por convecção forçada de ar através da sua superfície superior, que é a única não isolada pelo substrato.
A temperatura do ar é e o coeficiente de transferência de calor é . Sabendo-se que a temperatura da superfície superior do chip não pode exceder , responda qual é a maior potência que pode ser dissipada pelo chip.
Passo 1
Como a superfície inferior do chip é isolada termicamente, fazendo o balanço de energia no chip, temos que:
Nesse caso, temos apenas energia sendo gerada pelo chip e energia sendo retirada pela convecção entre o chip e o ar. Dessa forma:
Passo 2
A maior potência dissipada pelo chip será aquela quando o mesmo atingir a temperatura limite de . Dessa forma, a potência dissipada será:
Substituindo os valores:
![]()