Introdução à Trocadores de Calor
Teoria
Quem são? Onde vivem? Como se alimentam?
Basicamente, trocadores de calor são equipamentos utilizados pra troca de calor entre dois fluidos que estão em temperaturas diferentes e separados por uma parede sólida.
O fluido que entra com a maior temperatura é denominado fluido quente, enquanto o fluido que entra com a menor temperatura é o fluido frio.
O que diferencia os diversos tipos de trocadores de calor é a configuração do escoamento e o tipo de construção. Assim, eles podem ser classificados em:
- Trocadores de calor de escoamento paralelo;
- Trocadores de calor de escoamento contracorrente;
- Trocadores de calor de escoamento cruzado com aletas;
- Trocadores de calor de escoamento cruzado sem aletas;
- Trocadores de calor casco e tubos.
A imagem abaixo representa os trocadores de calor que acabamos de conhecer, se liga:
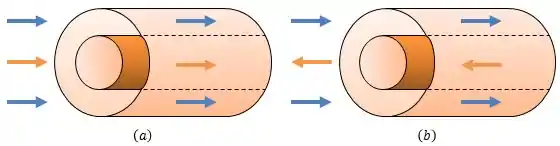
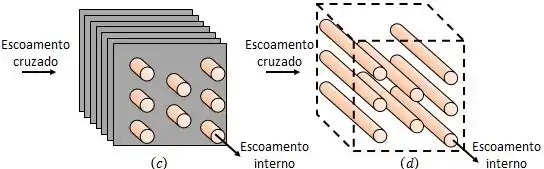
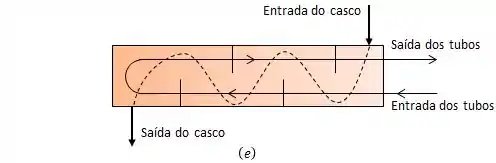
Repare que em todos os casos nós temos um escoamento interno e um escoamento externo, então tudo o que aprendemos sobre esses tópicos vai estar bastante presente aqui.
Como os problemas podem abordar os trocadores de calor?
Bom, já que fomos todos devidamente apresentados, já está na hora de brincar com um pouco com eles.
Então vamos supor que a gente tenha um tubo de aço inoxidável, com diâmetros interno e externo de , e comprimento , respectivamente, que é usado em um trocador de calor com escoamento cruzado.
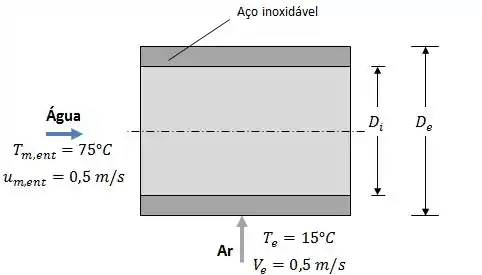
Considerando as seguintes propriedades para o ar:
E as seguintes propriedades para a água:
Considere a condutividade térmica do aço .
Obs.: Usei o índice porque estou me referindo à parede cilíndrica.
O que queremos saber é: qual é o coeficiente global de transferência de calor baseado na área externa do tubo ?
Bom, precisamos saber o que ele significa, certo?
Coeficiente Global de Transferência de Calor
De maneira geral, nos trocadores de calor a gente tem dois fluidos separados por uma parede (tubo ou placa) trocando calor entre eles. Então, na prática, a gente tem convecção no fluido quente, condução na parede sólida e convecção no fluido frio, se liga:
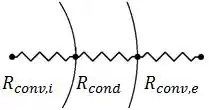
Onde os índices e fazem referência ao escoamento interno externo, respectivamente.
A gente chama a resistência térmica total de coeficiente global de troca térmica (), dada por.
Um detalhe muito importante é que o termo é constante tanto para a superfície interna, quanto para a superfície externa. Assim, o problema precisa dizer se devemos calcular o coeficiente global em relação à superfície interna , ou externa :
Ao passar do tempo, é comum que alguns sólidos se depositem na parede do trocador de calor. Isso acaba aumentando a resistência à passagem de calor, ou seja, a resistência térmica. Essa resistência térmica adicional é se chama fator de deposição .
Com isso a gente pode descrever esse aumento de resistência, acrescentando uma resistência na equação:
Onde e corresponde aos fatores de deposição para as superfície interna e externa, respectivamente.
Podemos ainda considerar a presença de aletas na parede, para aumentar a transferência de calor, como é o caso do trocador de calor . Assim, o coeficiente global é calculado por:
Onde o termo é a eficiência global da superfície, dada por:
Lembrando que é a área de todas as aletas, é a área total (aletas + base exposta) e é a eficiência de uma aleta.
Voltando ao nosso problema...
Como não estamos considerando fatores de deposição no nosso trocador e ele não possui aletas, podemos calcular o coeficiente global de transferência de calor dessa forma:
No nosso caso, estamos interessados em calcular o coeficiente global em relação à superfície externa, logo:
Como temos uma superfície cilíndrica, a resistência térmica de condução será, substituindo os valores:
Para a convecção interna, teremos o seguinte:
Para a convecção externa, teremos:
Substituindo todos os valores na expressão do coeficiente global, vamos encontrar o seguinte:
Onde e
Agora estamos prontos pra cair nos exercícios!
Como os problemas podem abordar os trocadores de calor?
Coeficiente Global de Transferência de Calor
Voltando ao nosso problema...
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Em uma caldeira flamatubular, produtos de combustão quentes, escoando através de uma matriz de tubos com paredes finas, são utilizados para ferver água escoando sobre os tubos. Quando da instalação, o coeficiente global de transferência de calor era igual a .
Após 1 ano de uso, há deposição sobre as superfícies interna e externa dos tubos, correspondendo a fatores de deposição de e , respectivamente.
Qual é o coeficiente global de transferência de calor após 1 ano de uso?
Passo 1
Como o enunciado nos disse que os tubos possuem paredes finas, não devemos levar em consideração a resistência térmica de condução. Além disso, isso implica que podemos considerar as áreas interna e externa do tubo iguais .
Assim, inicialmente, o coeficiente global de transferência de calor era dado por:
Após 1 ano de uso, temos que levar em consideração os fatores de deposição. Assim, o coeficiente global de transferência de calor passará a ser:
Passo 2
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um trocador de calor casco e tubos deve aquecer um líquido ácido que escoa em tubos não aletados com diâmetros interno e externo e , respectivamente.
Um gás quente escoa pelo casco. Para evitar corrosão no material dos tubos, o engenheiro pode especificar a utilização de uma liga metálica Ni-Cr-Mo resistente à corrosão , ou de fluoreto de polivinilideno (PVDF) , .
Os coeficientes de transferência de calor interno e externo são e , respectivamente.
Determine a razão entre as áreas das superfícies do plástico e do metal necessárias para transferir a mesma quantidade de calor.
Passo 1
Nesse caso, temos somente as convecções interna e externa e a condução através da parede do tubo. Assim, a expressão para o coeficiente global de transferência de calor será dada por:
Como estamos lidando com uma superfície cilíndrica, temos que:
Logo:
Passo 2
Vamos calcular cada termo separadamente, beleza? Começando pela convecção interna.
Para o termo de convecção externa, teremos:
Finalmente, para o termo de condução, vamos fazer logo as contas para o metal e para o fluoreto, se liga:
Passo 3
Para o metal, teremos o seguinte:
E, para o fluoreto:
Como o que queremos é a razão entre as áreas, teremos:
Como queremos transferir a mesma quantidade de calor nos dois casos, é necessário que:
Logo:
Finalmente:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Um equipamento para recuperação de calor envolve a transferência de energia dos gases quentes de exaustão, que passam através de uma região anular, para água pressurizada que escoa através do tubo interno da região anular.
Esse tubo interno possui diâmetros interno e externo de e e comprimento igual a , e está conectado a um tubo externo, isolado termicamente da vizinhança e com de diâmetro, por meio de oito barras de suporte.
Cada barra de suporte possui de espessura e é fabricada formando um conjunto integrado com o tubo interno em aço carbono .
Considere condições nas quais a água a escoa através do tubo interno a uma vazão de , enquanto os gases de exaustão a escoam através da região anular, mantendo um coeficiente convectivo de sobre as superfícies das barras de suporte e a superfície externa do tubo interno.
Qual é a taxa de transferência de calor do gás para a água?
Passo 1
A taxa de transferência de calor será dada por:
Onde, como temos um problema com aletas para o escoamento externo e sem fatores de deposição, o produto será dado por:
Vamos trabalhar com cada termo separadamente, beleza?
Passo 2
Para o termo de convecção interna, de acordo com a tabela A.4, considerando a temperatura de , temos as seguintes propriedades da água:
Assim, o número de Reynolds será:
Como temos um escoamento turbulento, a correlação mais adequada para o número de Nusselt, será:
Assim, o coeficiente convectivo será dado por:
Finalmente, o termo de convecção interna será:
Passo 3
Para o termo de condução, como estamos trabalhando com uma geometria cilíndrica, teremos:
Substituindo os valores:
Passo 4
Para o termo de convecção externa, teremos:
Como o problema já nos deu o coeficiente convectivo, temos apenas que calcular a eficiência global da superfície, dada por:
Onde:
Onde é o comprimento da aleta e é a sua altura.
Obs.: Multiplicamos a área por 8 pois são oito aletas, e por 2 pois estamos trocando calor com os dois lados da aleta.
Assim, a eficiência global da superfície será:
Logo:
Passo 5
Substituindo na expressão do coeficiente global de transferência de calor:
Passo 6
Assim, a taxa de transferência de calor será:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) O condensador de uma planta de potência a vapor possui tubos de latão , cada um com diâmetros interno e externo e , respectivamente.
A condensação do vapor d’água na superfície externa dos tubos é caracterizada por um coeficiente convectivo .
Se água de resfriamento vinda de um grande lado é bombeada através dos tubos do condensador a , qual é o coeficiente global de transferência de calor baseado na área da superfície externa do tubo?
Propriedades da água podem ser aproximadas como sendo , e .
Se, após uma longa operação, a deposição causa uma resistência de na superfície interna, qual é o valor de ?
Passo 1
Se água de resfriamento vinda de um grande lado é bombeada através dos tubos do condensador a , qual é o coeficiente global de transferência de calor baseado na área da superfície externa do tubo?
Inicialmente, como não há fatores de deposição, o coeficiente global de transferência de calor será dado pela seguinte equação:
Como e , podemos reescrever a equação acima da seguinte forma:
Vamos tratar de cada termo separadamente.
Passo 2
Para o termo de convecção interna, o número de Reynolds é dado por:
Como temos um escoamento turbulento, o número de Nusselt será dado por:
Assim, o coeficiente convectivo será dado por:
Finalmente, o termo de convecção interna será:
Passo 3
Para o termo de condução, como estamos trabalhando com uma geometria cilíndrica, teremos:
Substituindo os valores:
Assim:
Passo 4
Para o termo de convecção externa, teremos:
Passo 5
Substituindo todos os valores, o coeficiente global de transferência de calor, baseado na superfície externa, será:
Passo 6
Se, após uma longa operação, a deposição causa uma resistência de na superfície interna, qual é o valor de ?
Adicionando o fator de deposição na superfície interna, teremos:
Reorganizando os termos, novamente, teremos:
Opa! Mas tem uma galera aqui que já calculamos na letra , se liga:
Logo:
Substituindo os valores, teremos:
Resposta